Basic operations with complex numbers

Operations with complex numbers: Calculating with complex numbers

Basic operations with complex numbers

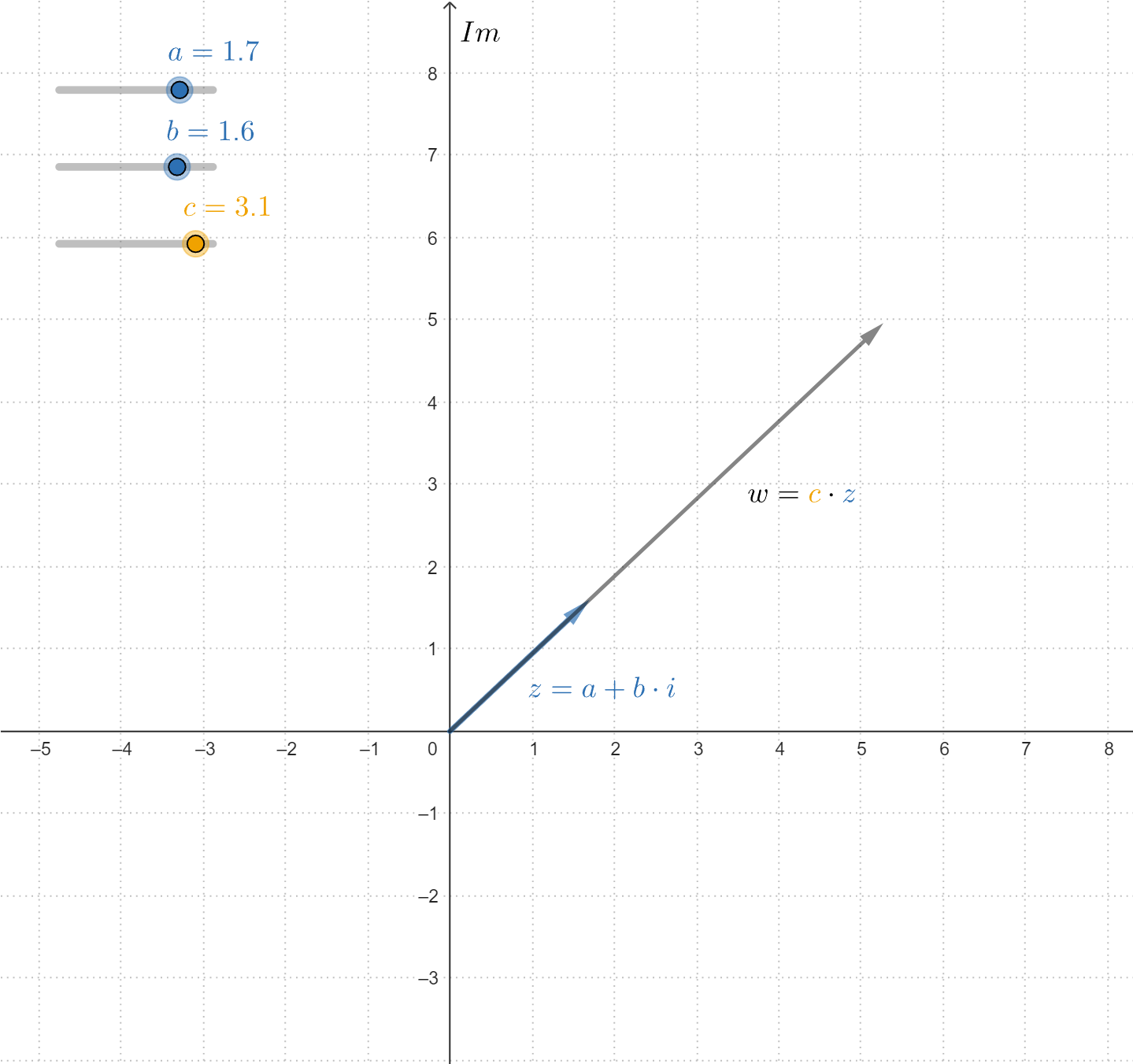
As with all other numbers we know, we can perform algebraic operations with complex numbers, such as addition, subtraction, multiplication, and division. On this page, we will explore these operations, leaving division for later. We start with multiplication by real scalars. When we multiply a complex number by a real number, we obtain a new complex number.

Multiplication by scalars

Let #\blue{z}=\blue{a+b\cdot \complexi}# and #\orange{c}# a real number.

The operation of multiplication by a scalar is defined as
\[\begin{array}{rcl}
\orange{c}\cdot \blue{z} &=& \orange{c}\cdot \left(\blue{a+b\cdot \complexi}\right) \\
&=&\orange{c}\cdot \blue{a} + \orange{c}\cdot \blue{b}\cdot \blue{\complexi}
\end{array}\]

Visually, this is represented as a stretch or shrink of the vector in the argand diagram.

Examples

\[\begin{array}{rcl}
\blue{z} &=& \blue{2 - \frac{1}{3} \cdot \ii} \\
\orange{3}\cdot \blue{z} &=& \orange{3} \cdot \blue{2} - \orange{3} \cdot \blue{\frac{1}{3} \cdot \ii}\\
&=& 6 - \ii \\
\orange{\frac{1}{2}}\cdot \blue{z} &=& \orange{\frac{1}{2}}\cdot \blue{2} - \orange{\frac{1}{2}}\cdot \blue{\frac{1}{3} \cdot \ii}\\
&=& 1 - \frac{1}{6} \cdot \ii \\
\end{array}\]

Visualisation

Note that in this way, each component of #\blue{z}# is scaled by #\orange{c}# and, therefore, multiplication by a scalar satisfies the distributive law. If we were to multiply #\blue{z}# by a complex number, then the result would not merely be a scaling of each component, as we will see later.

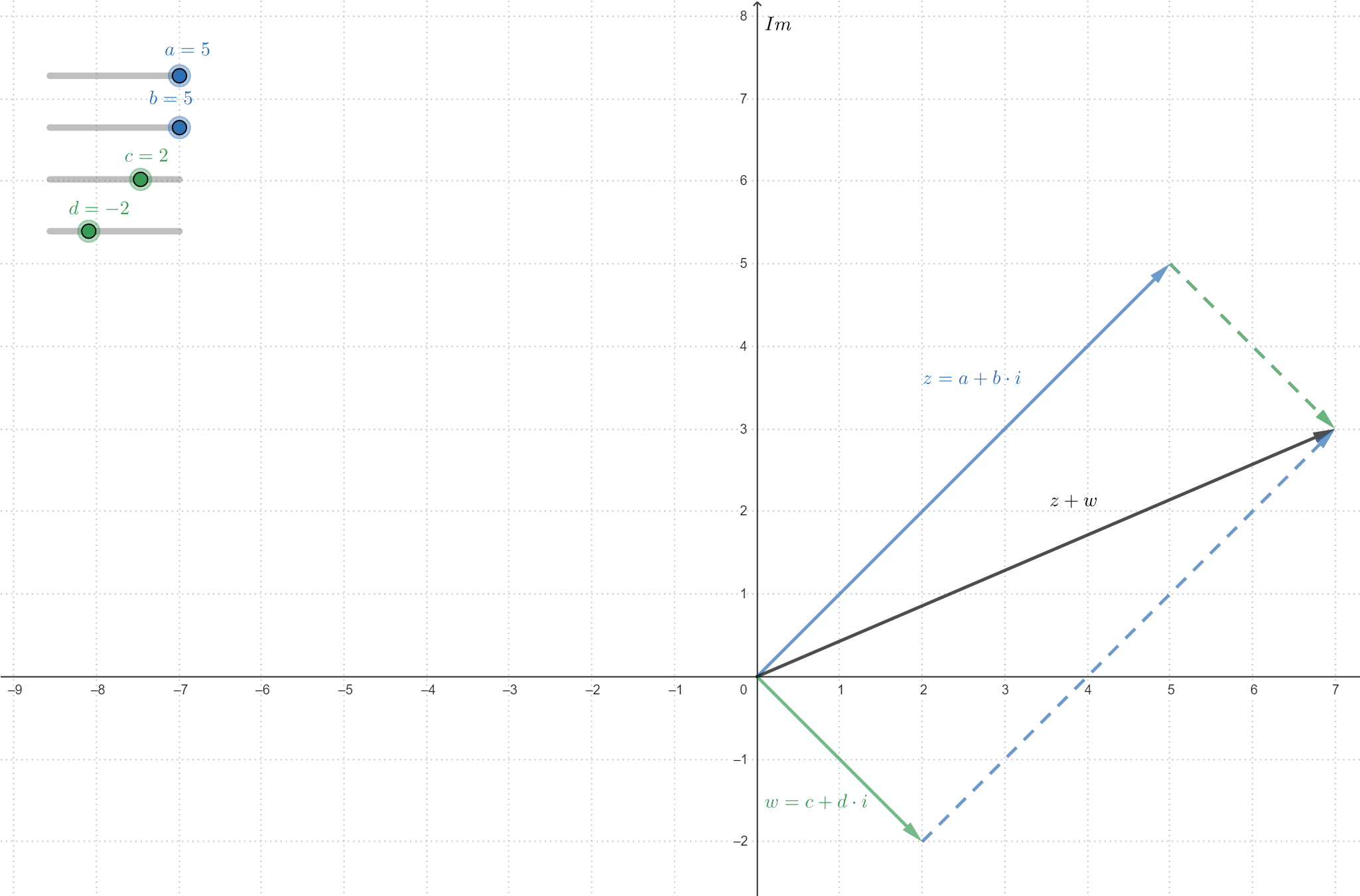
Next, we address addition and subtraction of complex numbers. When we add (or subtract) two complex numbers, the real and imaginary parts of the result are respectively given by the sum (or subtraction) of the real and imaginary parts of the original numbers.

Addition and subtraction

Let #\blue{z}=\blue{a+b\cdot \complexi}# and #\green{w} = \green{c + d\cdot \complexi}#.

Their addition is defined as

\[\begin{array}{rcl}
\blue{z} + \green{w} &=& \left(\blue{a+b\cdot \complexi}\right) + \left( \green{c + d\cdot \complexi}\right)\\ &=& \left(\blue{a} + \green{c}\right) + \left(\blue{b} + \green{d}\right)\cdot \complexi \end{array}\]

Their subtraction is defined as

\[\begin{array}{rcl}
\blue{z} - \green{w} &=& \left(\blue{a+b\cdot \complexi}\right) - \left( \green{c + d\cdot \complexi}\right)\\ &=& \left(\blue{a} - \green{c}\right) + \left(\blue{b} - \green{d}\right)\cdot \complexi\end{array}\]

Examples

\[\begin{array}{rcl}
\blue{z} &=& \blue{2 - 5 \cdot \ii} \\
\green{w} &=& \green{-1 + 3 \cdot \ii} \\ \\
\blue{z}+\green{w} &=& (\blue{2}+(\green{-1})) + (\blue{-5}+\green{3}) \cdot \ii\\
&=& 1 -2 \cdot \ii \\ \\
\blue{z}-\green{w} &=& (\blue{2}-(\green{-1})) + (\blue{-5}-\green{3}) \cdot \ii\\
&=& 3 -8 \cdot \ii
\end{array}\]

In the Argand diagram, the addition of two complex numbers is represented as placing their vectors head-to-tail with the resultant vector representing the sum.

Note

Note that we would have obtained the same result #\blue{z}-\green{w}# if we had instead multiplied #\green{w}# by #-1# and then added the result to #\blue{z}#.

Visualisation addition

Visualisation subtraction

Having defined and visualised the sum and difference of complex numbers, let us now address their product. The multiplication of complex numbers follows exactly as can be expected from real numbers. As we show in the box, the real part of the product of two complex numbers contains not just the product of their respective real parts but also the product of their respective imaginary parts.

Multiplication of complex numbers

Let #\blue{z}=\blue{a + b\cdot \complexi}# and #\green{w} = \green{c + d\cdot \complexi}#. Then, #\blue{z}\cdot \green{w}# is given by

\[\begin{array}{rcl}
\blue{z}\cdot \green{w} &=& \left(\blue{a+b\cdot \complexi}\right) \cdot \left(\green{c+d\cdot \complexi}\right) \\&=&\blue{a}\cdot \green{c} + \blue{a}\cdot \green{d}\cdot \complexi + \blue{b}\cdot\green{c}\cdot \complexi +\blue{b}\cdot\green{d}\cdot\left(\complexi^2\right)\\&=& \left(\blue{a}\cdot \green{c} - \blue{b}\cdot \green{d}\right) + \left(\blue{a}\cdot \green{d} + \blue{b}\cdot \green{c}\right)\cdot \complexi\end{array}\]

Example

\[\begin{array}{rcl}
\blue{z} &=& \blue{2 + 4 \cdot \ii} \\
\green{w} &=& \green{1 + 3 \cdot \ii} \\ \\
\blue{z}\cdot \green{w} &=& \left(\blue{2}\cdot \green{1} - \blue{4}\cdot \green{3}\right) \\
&&\quad + \left(\blue{2}\cdot \green{3} + \blue{4}\cdot \green{1}\right)\cdot \ii \\
&=& -10+10 \cdot \ii
\end{array}\]

Powers of z

As with real numbers, the powers of complex numbers consist in the repeated multiplication of the number by itself. \[\blue{z}^{\orange{n}} = \underbrace{\blue{z}\cdot \blue{z}\cdot \blue{z}\cdot \ldots \cdot \blue{z}}_{\orange{n} \text{ times}}\]

Examples:
\[\begin{array}{rcl}\blue{z}^{\orange{2}} &=&\left(a + b\cdot \complexi\right)\cdot\left(a + b\cdot \complexi\right)\\
&=&a^2+2\cdot a\cdot b\cdot \complexi + b\cdot \complexi^2\\&=& a^2 + 2\cdot a\cdot b\cdot \complexi - b^2\\&&\\
\blue{z}^{\orange{3}} &=& \blue{z}\cdot \blue{z}^2\\
&=&\left(a+b\cdot \complexi\right) \cdot \left(a^2 +2\cdot a\cdot b\cdot \complexi - b^2 \right)\\
&=&a^3+2\cdot a^2\cdot b\cdot \complexi -b^2 \cdot a \\&&+\,b\cdot a^2\cdot \complexi + 2\cdot a\cdot b^2\cdot \complexi^2-b^3\cdot \complexi\\
&=& a^3 +3\cdot a^2\cdot b\cdot \complexi - 3\cdot a\cdot b^2 - b^3\cdot \complexi\end{array}\]

As we can see, multiplication of complex numbers satisfies the same distributive laws as that of real numbers.

Write the sum of the two complex numbers \[-4-4\cdot \complexi \qquad\text{and}\qquad 1+2\cdot \complexi\] in cartesian form.

#-3-2\cdot \complexi#

#\begin{array}{rcl}
(-4-4\cdot \complexi) + (1+2\cdot \complexi) &=& (-4+1) + (-4+2) \cdot \complexi \\
&&\qquad\blue{\text{combined like terms}} \\
&=& -3-2\cdot \complexi \\
&&\qquad\blue{\text{simplified}}
\end {array}#

New example