Differentiaalvergelijkingen: Scheiden van variabelen
 Differentiaalvormen en gescheiden variabelen
Differentiaalvormen en gescheiden variabelen
We hebben gezien dat het vinden van een primitieve van de functie #f(t)# kan worden geformuleerd als het oplossen van de eerste orde differentiaalvergelijking #y'=f(t)#. Een effectieve tussenstap van de GDV naar de oplossing bleek de differentiaalvorm #\dd y = f(t)\,\dd t# te zijn. Er zijn meer GDVs van de eerste orde die kunnen worden opgelost met behulp van de differentiaalvorm.
Scheiding van variabelen
Stel dat \(f(t)\) en \(g(y)\) continue functies zijn, met #g(y)# ongelijk aan de constante functie #0#, dat \(F(t)\) een primitieve is van #f(t)# en dat \(H(y)\) een primitieve is van #\frac{1}{g(y)}#.
De algemene oplossing #y# van de differentiaalvergelijking \[y'(t)={g(y)}\cdot{f(t)}\] voldoet aan de gelijkheid \[H(y)=F(t)+C\] waarbij \(C\) een constante is.
In het algemeen is dit geen oplossing van de GDV in de expliciete vorm \( y(t)=\text{een functie van }t\), maar een relatie tussen de variabelen \(y\) en \(t\). Soms kun je een expliciete oplossing uit deze relatie afleiden.
Scheidbare differentiaalvergelijking
Laat #y# een differentieerbare functie van #t# zijn. Een scheidbare differentiaalvergelijking is een eerste orde differentiaalvergelijking van de eerste graad waarin de afgeleide \(y'\) ontbonden kan worden als een product van een functie \(g(y)\) van de onbekende afhankelijke variabele \(y\) en een functie \(f(t)\) van de onafhankelijke variabele \(t\): \[ y '(t) = g(y) \cdot f(t) \]
Een oplossing als #H(y)=F(t)+C# van bovenstaande stelling wordt vaak aangeduid als een impliciete oplossing van de GDV.
Als er beginwaarden zijn, dan kan de impliciete oplossing worden gebruikt om corresponderende waarden voor #C# te vinden.
Hieronder staan enkele voorbeelden. Hierna bespreken we de methode uitvoeriger en behandelen we meer voorbeelden.
#y= \dfrac{1}{3}\; t + 1#
De differentiaalvergelijking is scheidbaar, want met \(g(y) = \frac{1}{3} \) en \(f(t) = 1 \) kunnen we haar herschrijven als
\[\displaystyle \int 3\; \dd y = \displaystyle \int 1\; \dd t \]
Na berekening van de primitieve functies krijgen we
\[ 3 y = t + C \]
Door beide zijden te vermenigvuldigen met \(\frac{1}{3}\) vinden we
\[ y = \dfrac{1}{3}\; t + C \]
Dit is de algemene oplossing van de differentiaalvergelijking.
Deze oplossing geeft een klasse van functies, die allemaal groeifactor eenderde hebben. Meetkundig kunnen wij de klasse van functies met het volgende richtingsveld beschrijven.
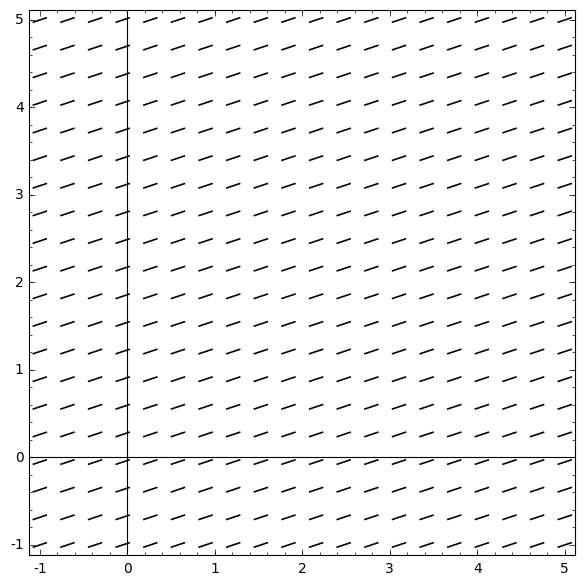
Om een specifieke oplossing te vinden, lossen we het beginwaardeprobleem op met de beginvoorwaarde \( \rv{t,y} = \rv{0,1}\). Na substitutie van de waarden \(y=1\) en \(t=0\) vinden we
\[ 1 = \dfrac{1}{3}\; \cdot 0 + C \]
Daarom hebben we \(C = 1\), zodat de overeenkomstige specifieke oplossing de volgende functie is:
\[ y = \dfrac{1}{3}\; t + 1 \]
De grafiek van deze functie is hieronder grafisch weergegeven als een lijn in het lijnelementenveld:
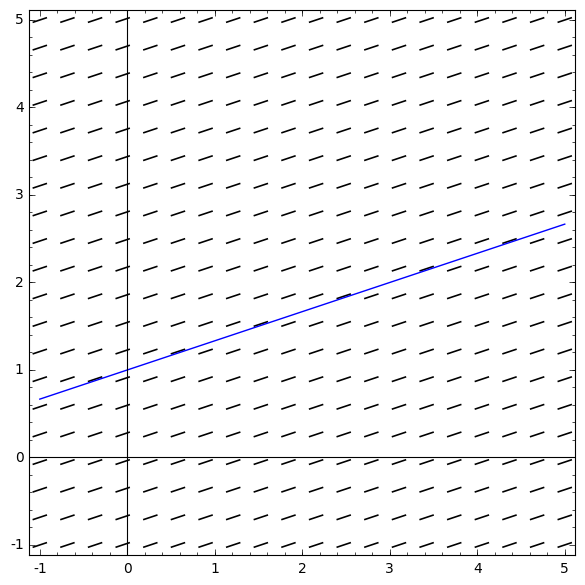

omptest.org als je een OMPT examen moet maken.



