Quadratic equations: Intersection points of parabolas
 Intersection points of a parabola with a line
Intersection points of a parabola with a line
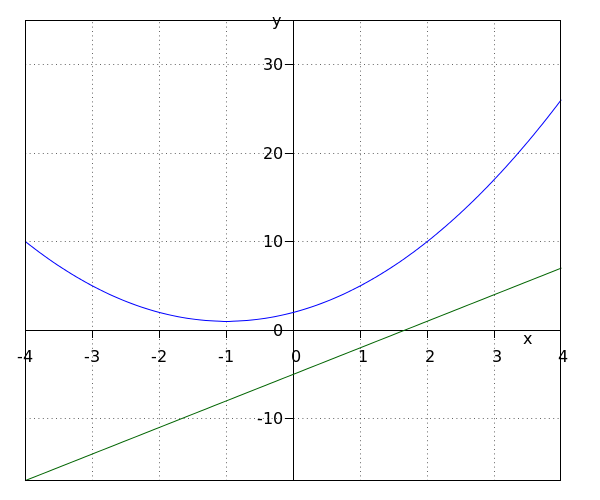
A quadratic formula #y=a_1x^2+b_1x+c_1# and a linear formula #y=a_2x+b_2# can have zero, one or two intersection points. We will now investigate how to find these intersection points.
Intersection points parabola and line
| Procedure |
geogebra plaatje
|
|
|
We determine the intersection point of the parabola #y=a_1x^2+b_1x+c_1# and the line #y=a_2x+b_2#. |
||
| Step 1 |
First, we determine the #x#-coordinate of the intersection point by solving the equation \[a_1x^2+b_1x+c_1=a_2x+b_2\] by means of factorization, completing the square or the quadratic formula. |
|
| Step 2 |
We determine the #y#-coordinate of the intersection point by substituting the obtained #x#-coordinate in one of both formulas. Usually, it is easier to substitute in the linear formula. |
The last step indicates that given the graphs \[y = -x^2-8\cdot x\phantom{xxx}\text{ and }\phantom{xxx} y = -x\]
intersect each other at two points. Determine the two intersection points.
Give your answer in the form #\left\{\rv{a,b},\rv{c,d}\right\}#, in which #a#, #b#, #c#, #d# are exact numbers.
intersect each other at two points. Determine the two intersection points.
Give your answer in the form #\left\{\rv{a,b},\rv{c,d}\right\}#, in which #a#, #b#, #c#, #d# are exact numbers.
#\left \{\rv{ -7 , 7 } , \rv{ 0 , 0 } \right \} #
The #x#-coordinate of a point lying on both parabolas must satisfy
\[-x^2-8\cdot x = -x\tiny.\]
We solve this equation, after reduction, by factorization.
\[\begin{array}{rcl}
-x^2-7\cdot x &=& 0\\
&&\phantom{xxx}\blue{\text{all terms to the left hand side}}\\
x^2+7\cdot x &=& 0\\ &&\phantom{xxx}\color{blue}{\text{left and right hand side multiplied by -1 }}\\
x\cdot \left(x+7\right) &=&0 \\
&&\phantom{xxx}\blue{\text{factorized}}\\
x = 0 &\lor& x+7=0 \\
&&\phantom{xxx}\blue{A\cdot B=0 \text{ if and only if }A=0\lor B=0}\\
x=0 &\lor& x=-7 \\
&&\phantom{xxx}\blue{\text{constant term to the right hand side}}\\
\end{array}\]
Now, we can calculate the corresponding #y#-value by entering this #x#-value in one of both formulas. In this case, it is most convenient to choose the linear function. First, we calculate the #y#-value at #x=-7#.
\[\begin{array}{rcl}
y&= & -\left(-7\right) = 7
\end{array}\]
Next, we calculate the #y#-value at #x=0#.
\[\begin{array}{rcl}
y&=& 0
\end{array}\]
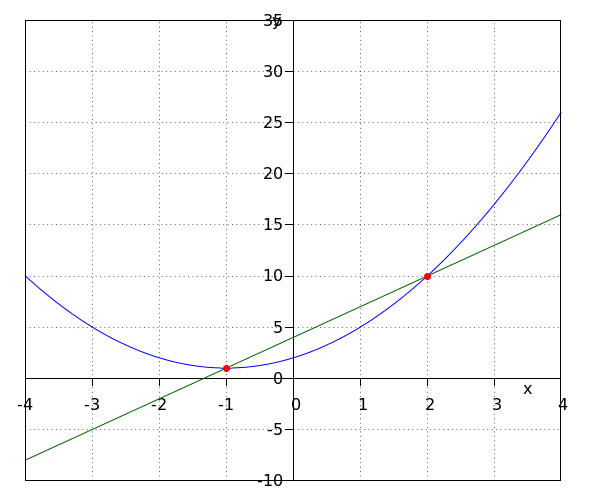
The conclusion is that the #2# points of intersection are given by: \[ \left \{\rv{ -7 , 7 } , \rv{ 0 , 0 } \right \}\tiny. \]
The #x#-coordinate of a point lying on both parabolas must satisfy
\[-x^2-8\cdot x = -x\tiny.\]
We solve this equation, after reduction, by factorization.
\[\begin{array}{rcl}
-x^2-7\cdot x &=& 0\\
&&\phantom{xxx}\blue{\text{all terms to the left hand side}}\\
x^2+7\cdot x &=& 0\\ &&\phantom{xxx}\color{blue}{\text{left and right hand side multiplied by -1 }}\\
x\cdot \left(x+7\right) &=&0 \\
&&\phantom{xxx}\blue{\text{factorized}}\\
x = 0 &\lor& x+7=0 \\
&&\phantom{xxx}\blue{A\cdot B=0 \text{ if and only if }A=0\lor B=0}\\
x=0 &\lor& x=-7 \\
&&\phantom{xxx}\blue{\text{constant term to the right hand side}}\\
\end{array}\]
Now, we can calculate the corresponding #y#-value by entering this #x#-value in one of both formulas. In this case, it is most convenient to choose the linear function. First, we calculate the #y#-value at #x=-7#.
\[\begin{array}{rcl}
y&= & -\left(-7\right) = 7
\end{array}\]
Next, we calculate the #y#-value at #x=0#.
\[\begin{array}{rcl}
y&=& 0
\end{array}\]
The conclusion is that the #2# points of intersection are given by: \[ \left \{\rv{ -7 , 7 } , \rv{ 0 , 0 } \right \}\tiny. \]
We see that the calculated intersection points match the intersection points identified in step 1. See the figure below, in which the intersection points are drawn in red.


Unlock full access


Teacher access
Request a demo account. We will help you get started with our digital learning environment.
Student access
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.