To describe the motion of an object, you must first be able to describe its position, where it is at any particular time. More precisely, you need to specify its position relative to a convenient reference frame. Earth is often used as a reference frame, and we often describe the position of an object as it relates to stationary objects in that reference frame.
For example, a rocket launch would be described in terms of the position of the rocket with respect to the Earth as a whole, while a professor’s position could be described in terms of where she is in relation to the nearby whiteboard (see Figure 1). In other cases, we use reference frames that are not stationary but are in motion relative to the Earth. To describe the position of a person in an airplane, for example, we use the airplane, not the Earth, as the reference frame (see Figure 2).
Note: the examples discussed here refer to the figures found below. Do not worry about the symbols on the pictures for now, they will have been explained by the time you get there.
If an object moves relative to a reference frame (for example, if a professor moves to the right relative to a whiteboard or a passenger moves toward the rear of an airplane), then the object’s position changes. This change in position is known as displacement. The word “displacement” implies that an object has moved or has been displaced. We define the concept below.
#\textbf{Displacement}# is the change in position of an object:
\[\begin{array}{rcl}\blue{\Delta x}&=&\green{{x}_f}-\orange{{x}_{0}}\end{array}\]
where #\blue{\Delta x}# is displacement, #\green{{x}_f}# is the #\textbf{final position}#, and #\orange{{x}_{0}}# is the #\textbf{initial position}#.
In this text, the upper case Greek letter #\blue{\Delta }# (delta) always means “change in” whatever quantity follows it; thus, #\blue{\Delta x}# means change in position. Always solve for displacement by subtracting initial position #\orange{{x}_{0}}# from final position #\green{{x}_f}# .
Note that the SI unit for displacement is the meter (#\unit{\!}{m}#) (see Physical quantities and units), but sometimes kilometers, miles, feet, and other units of length are used. Keep in mind that when units other than the meter are used in a problem, you may need to convert them into meters to complete the calculation.
Let us look at an example.
Fig. 1 A professor paces left and right while lecturing. Her position relative to Earth is given by #x#. The #\blue{+2.0\mathrm{\ m}}# displacement of the professor relative to Earth is represented by an arrow pointing to the right.
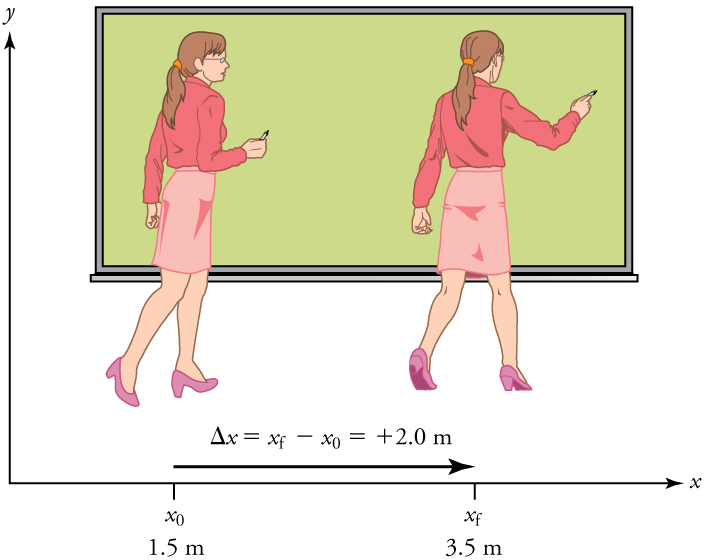
In the example displayed above, the professor’s initial position is #\orange{{x}_{0}}=\orange{\unit{1.5}{m}}# and her final position is #\green{{x}_f}=\green{\unit{3.5}{m}}#. Thus her displacement is
\[ \begin{array}{rcl}\blue{\Delta x}=\green{{x}_f}-\orange{{x}_{0}}=\green{3.5}-\orange{1.5 }=\blue{\unit{+2.0}{ m}}\end{array}\]
In this coordinate system, motion to the right is positive, whereas motion to the left is negative. As we will see below, a choice of positive direction must always be made.
Displacement has a direction as well as a magnitude. Below, we discuss how to find this direction.
In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually, that will be to the right or up, but you are free to select positive as being any direction).
Values on the direction you have selected as positive are either written as they are or with a plus sign, e.g., in the example above the initial position, #\orange{x_0}#, can either be written as #\orange{x_0}=\orange{\unit{1.5 }{m}}# or #\orange{x_0}=\orange{\unit{+1.5 }{m}}#. Values on the direction you have selected as negative are always preceded by a minus sign.
Let us look at another example.
Fig. 2 A passenger moves from his seat to the back of the plane. His location relative to the airplane is given by #x#. The #\blue{-4.0\mathrm{\ m}}# displacement of the passenger relative to the plane is represented by an arrow toward the rear of the plane. Notice that the arrow representing his displacement is twice as long as the arrow representing the displacement of the professor (he moves twice as far) in Figure 1.
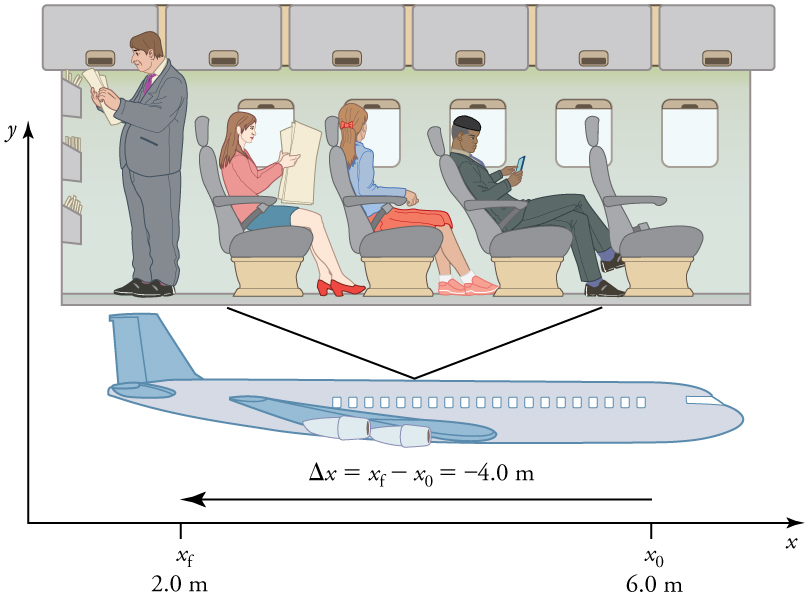
In the example displayed above, the airplane passenger’s initial position is #\orange{{x}_{0}}=\orange{\unit{6.0}{ m}}# and his final position is #\green{{x}_f}=\green{\unit{2.0}{m}}#, so his displacement is
\[ \begin{array}{rcl}\blue{\Delta x}=\green{{x}_f}-\orange{{x}_{0}}=\green{2.0}-\orange{6.0}=\blue{\unit{-4.0}{ m}}\end{array} \]
His displacement is negative because his motion is toward the rear of the plane, or in the negative #x# direction in our coordinate system.
Although displacement is described in terms of direction, distance, which we define next, is not.
The distance is defined to be the magnitude or size of displacement between two positions.
Note that the distance between two positions is not the same as the distance traveled between them. Distance traveled is the total length of the path traveled between two positions.
Distance has no direction and, thus, no sign. In the second example shown above, the distance the professor walks is #\unit{2.0}{m}#, while the distance the airplane passenger walks is #\unit{4.0}{m}#.
It is important to note that the distance traveled, however, can be greater than the magnitude of the displacement (by magnitude, we mean just the size of the displacement without regard to its direction; that is, just a number with a unit). For example, the professor could pace back and forth many times, perhaps walking a distance of #\unit{150}{m}# during a lecture, yet still end up only #\unit{2.0}{m}# to the right of her starting point. In this case, her displacement would be #\unit{+2.0}{m}#, the magnitude of her displacement would be #\unit{2.0}{m}#, but the distance she traveled would be #\unit{150}{m}#. In kinematics, we nearly always deal with displacement and its magnitude and almost never with distance traveled. One way to think about this is to assume you marked the start of the motion and the end of the motion. The displacement is simply the difference in the position of the two marks and is independent of the path taken when traveling between the two marks. The distance traveled, however, is the total length of the path taken between the two marks.
Compute the displacement given the following initial and final positions:
\[\begin{array}{rcl}
\orange{x_0}&=&\orange{\unit{10}{m}}\\
\green{x_f}&=&\green{\unit{-4}{m}}
\end{array}\]
Recall that the displacement, #\blue{\Delta x}#, is the difference between the final position, #\green{x_f}#, and the initial position, #\orange{x_0}#. Hence,
\[\begin{array}{rcl}
\blue{\Delta x}&=&\green{x_f}-\orange{x_0} \\&&\quad\blue{\text{definition of displacement}}\\
&=& \green{-4}-\orange{10}\\
&& \quad\blue{\text{filled in numerical values}}\\
&=&\blue{\unit{-14}{m}} \\&&\quad\blue{\text{computed}}\\
\end{array}\]
Displacement
