Motion in two dimensions: an introduction

[OpenStax College Physics 2e: Two-dimensional kinematics] Two-dimensional motion: Introduction to two-dimensional motion

Motion in two dimensions: an introduction

Two-dimensional motion: walking in a city

Suppose you want to walk from one point to another in a city with uniform square blocks, as pictured in Figure 1.

Fig. 1 A pedestrian walks a two-dimensional path between two points in a city. In this scene, all blocks are square and are the same size.

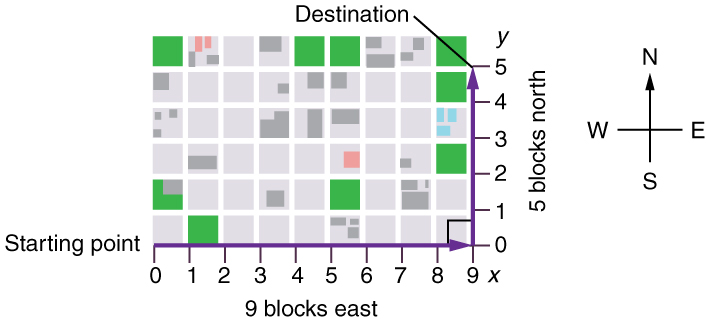
The straight-line path that a helicopter might fly is blocked to you as a pedestrian, and so you are forced to take a two-dimensional path, such as the one shown. You walk #{14}# blocks in all, #\green{9}# east followed by #\orange{5}# north.

The example above serves as a motivation to try and compute straight-line distance between the starting point and the destination.

Straight line distance

An old adage states that the shortest distance between two points is a straight line. The two legs of the trip and the straight-line path form a right triangle, and so the Pythagorean theorem, #\green{a}^{2}+\orange{b}^{2}=\blue{c}^{2}#, can be used to find the straight-line distance.

Fig. 2 The Pythagorean theorem relates the length of the legs of a right triangle, labeled #\green{a}# and #\orange{b}#, with the hypotenuse, labeled #\blue{c}#. The relationship is given by: #\green{a}^{2}+\orange{b}^{2}=\blue{c}^{2}#. By solving for #\blue{c}#, this can be rewritten as #\blue{c}=\sqrt{\green{a}^{2}+\orange{b}^{2}}#.

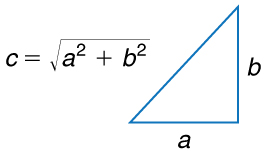
Returning to the first example, the hypotenuse of the triangle is the straight-line path, and so in this case its length in units of city blocks is \[\sqrt{(\green{9})^{2}+(\orange{5})^{2}}= \unit{\blue{10.3}}{\text{blocks}}\] which is considerably shorter than the #{14}# blocks you walked.

Fig. 3 The straight-line path followed by a helicopter between the two points is shorter than the #{14}# blocks walked by the pedestrian. All blocks are square and the same size.

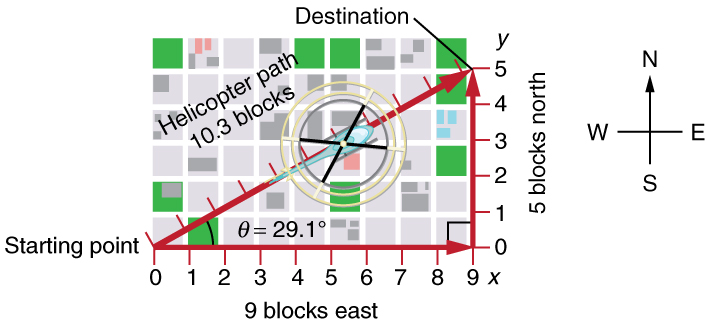
Distance walked vs straight-line distance

The fact that the straight-line distance, #\unit{\blue{10.3}}{\text{blocks}}#, in Figure 3 is less than the total distance walked #\unit{{14}}{\text{blocks}}#, is one example of a general characteristic of vectors. In terms of triangles, it says that the length of the hypotenuse is always smaller or equal to the sum of the lengths of the adjacent and opposite sides.

Note on significance

Note that we are using three significant figures in the answer. Although it appears that “#9#” and “#5#” have only one significant digit, they are discrete numbers. In this case “#9# blocks” is the same as “#9.0# blocks” or “#9.00# blocks.” We have decided to use three significant figures in the answer in order to show the result more precisely.

As for one-dimensional motion, we use arrows to represent vectors. The length of the arrow is proportional to the vector’s magnitude. The arrow’s length is indicated by hash marks in Figure 1 and Figure 3. The arrow points in the same direction as the vector.

Two-dimensional vectors

For two-dimensional motion, the path of an object can be represented with three vectors: one vector shows the straight-line path between the initial and final points of the motion, one vector shows the horizontal component of the motion, and one vector shows the vertical component of the motion. The horizontal and vertical components of the motion add together to give the straight-line path.

Example

For example, observe the three vectors in Figure 3. The first represents a #9#-block displacement east. The second represents a #5#-block displacement north. These vectors are added to give the third vector, with a #10.3#-block total displacement. The third vector is the straight-line path between the two points.

Addition of non-perpendicular vectors

In this example, the vectors that we are adding are perpendicular to each other and thus form a right triangle. This means that we can use the Pythagorean theorem to calculate the magnitude of the total displacement.

Note that we cannot use the Pythagorean theorem to add vectors that are not perpendicular. We will develop techniques for adding vectors having any direction, not just those perpendicular to one another, in Vector addition and subtraction: graphical methods and Vector addition and subtraction: analytical methods.

The independence of perpendicular motions

The person taking the path shown in Figure 3 walks east and then north (two perpendicular directions). How far they walk east is only affected by their motion eastward. Similarly, how far they walk north is only affected by their motion northward. In other words, motion along a given direction is independent of what happens along a perpendicular direction.

Independence of motion

The horizontal and vertical components of two-dimensional motion are independent of each other. Any motion in the horizontal direction does not affect motion in the vertical direction, and vice versa.

This is true in a simple scenario like that of walking in one direction first, followed by another. It is also true of more complicated motion involving movement in two directions at once.

As an example, let us compare the motion of two baseballs.

Independent motions of a falling ball

One baseball is dropped from rest. At the same instant, another is thrown horizontally from the same height and follows a curved path. A stroboscope has captured the positions of the balls at fixed time intervals as they fall.

Fig. 4 This shows the motion of two identical balls: the ball on the right has an initial horizontal velocity, while the ball on the left has no horizontal velocity. Each subsequent position is an equal time interval. Arrows represent horizontal and vertical velocities at each position. Despite the difference in horizontal velocities, the vertical velocities and positions are identical for both balls. This shows that the vertical and horizontal motions are independent.

It is remarkable that for each flash of the strobe, the vertical positions of the two balls are the same. This similarity implies that the vertical motion is independent of whether or not the ball is moving horizontally.

Discussion

Vertical motion is not influenced by horizontal forces and, assuming no air resistance, is influenced by gravity only. Careful examination of the ball thrown horizontally shows that it travels the same horizontal distance between flashes. This is due to the fact that there are no additional forces on the ball in the horizontal direction after it is thrown. This result means that the horizontal velocity is constant, and affected neither by vertical motion nor by gravity (which is vertical). Note this case is true only for ideal conditions. In the real world, air resistance will affect the speed of the balls in both directions.

The two-dimensional curved path of the horizontally thrown ball is composed of two independent one-dimensional motions (horizontal and vertical).

Resolving motion

The key to analyzing such motion, called projectile motion, is to resolve (break) it into motion along perpendicular directions. Resolving two-dimensional motion into perpendicular components is possible because the components are independent.

We shall see how to resolve vectors in Vector addition and subtraction: graphical methods and Vector addition and subtraction: analytical methods. We will find such techniques to be useful in many areas of physics.