Projectile motion I

[OpenStax College Physics 2e: Two-dimensional kinematics] Two-dimensional motion: Two-dimensional motion

Projectile motion I

Projectile motion

Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. The object is called a projectile, and its path is called its trajectory.

The motion of falling objects, as covered in Falling objects, is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In this page, we consider two-dimensional projectile motion, such as that of a football, and we assume that air resistance is negligible for all objects treated. The most important fact to remember here is that motions along perpendicular axes are independent and, thus, can be analyzed separately. This fact was discussed in Introduction to two-dimensional motion, where vertical and horizontal motions were seen to be independent.

The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. This choice of axes is the most sensible, because acceleration due to gravity is vertical, thus, there will be no acceleration along the horizontal axis when air resistance is negligible. As is customary, we call the horizontal axis the #x#-axis and the vertical axis the #y#-axis.

Notation
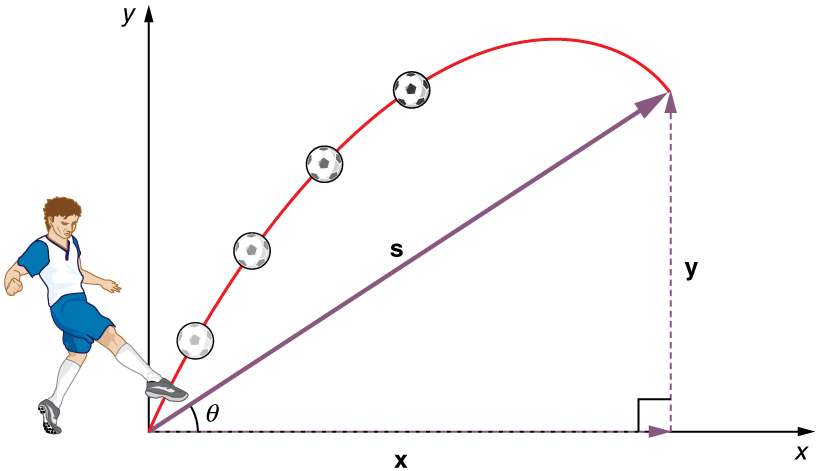
Figure 1 illustrates the notation for displacement, where #\blue{\blue{\vec{s}}}# is defined to be the total displacement
\[\blue{\vec{s}} = \blue{\vec{s}_0} + \orange{\vec{v}_0}\cdot t + \dfrac{1}{2}\cdot\purple{\vec{a}}\cdot t^2\]
Its components along the horizontal and vertical axes are #\blue{\vec{x}}# and #\blue{\vec{y}}#, respectively. The magnitudes of these vectors are #\blue{\norm{s}}#, #\blue{\norm{x}}#, and #\blue{\norm{y}}#, respectively.

Fig. 1 The total displacement #\blue{\vec{s}}# of a football ball at a point along its path. The vector #\blue{\vec{s}}# has components #\blue{\vec{x}}# and #\blue{\vec{y}}# along the horizontal and vertical axes. Its magnitude is #\blue{\norm{s}}#, and it makes an angle #\green{\theta} # with the horizontal.

Of course, to describe motion, we must deal with velocity and acceleration, which are related by the equation
\[\orange{\vec{v}} = \orange{\vec{v}_0} + \purple{\vec{a}}\cdot t\]
We must find their components along the #x#- and #y#-axes, too. We will assume all forces except gravity (such as air resistance and friction, for example) are negligible. The components of acceleration are then very simple: #\purple{a_y}=–\purple{g}=–\purple{\unit{9.81}{m/s^{2}}}#. Note that this definition assumes that the upward direction is defined as the positive direction. If you arrange the coordinate system instead such that the downwards direction is positive, then acceleration due to gravity takes a positive value. Because gravity is vertical, #\purple{a_x}=\purple{0}#.

Note that earlier in the chapter, we used the notation #\vec{A}# to represent a vector with components #{\vec{A}}_{x}# and #{\vec{A}}_{y}#. If we continued this format, we would call displacement #\blue{\vec{s}}# with components #\blue{\vec{s}_{x}}# and #\blue{\vec{s}_{y}}#. However, to simplify the notation, we will simply represent the component vectors as #\blue{\vec{x}}# and #\blue{\vec{y}}#.

Review of equations of motion (constant a)
Because both accelerations are constant, the equations of motion from the last chapter can be used. Below, find a summary of the equations from one-dimensional motion:
\[ \begin{array}{rcl}\blue{x} &=&\blue{{x}_{0}}+\orange{\bar{v}}\cdot t\\
\orange{\bar{v}}&=&\dfrac{\orange{v_0}+\orange{v}}{2}\\
\orange{\bar{v}}&=&\orange{v_0}+\purple{a}\cdot t\\
\blue{x} &=&\blue{{x}_{0}}+\orange{v_0}\cdot t+\dfrac{1}{2}\cdot \purple{a}\cdot t^{2}\\
\blue{v}^{2}&=&\orange{{v}}_\orange{\mathrm{0}}^2+2\cdot \purple{a}\cdot (\blue{x} -\blue{{x}_{0}})
\end{array}\]

Analysis of projectile motion

Given these assumptions, the following steps are then used to analyze projectile motion.

Step 1 Resolve or break the motion into horizontal and vertical components along the #x#- and #y#-axes. Since the axes are perpendicular, we use
\[ {A}_{x}=\norm{\vec{A}}\cdot \cos\green{\theta}\quad\text{and}\quad {A}_{y}=\norm{\vec{A}}\cdot \sin\green{\theta} \]
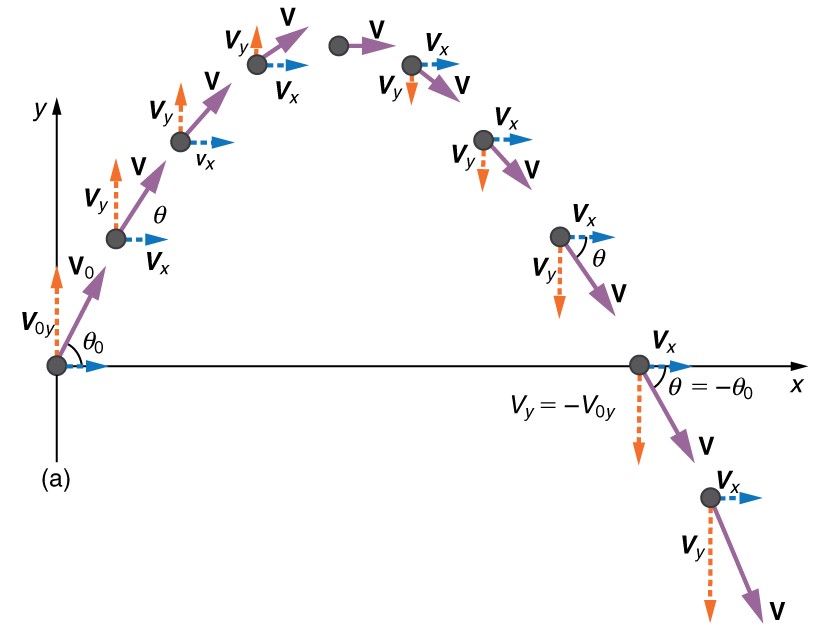
The magnitude of the components of displacement #\blue{\vec{s}}# along these axes is #\blue{\norm{x}}# and #\blue{\norm{y}}#. The magnitudes of the components of the velocity #\orange{\vec{v}}# are #\orange{v_x}=\norm{\orange{\vec{v}}}\cdot\cos\green{\theta} # and #\orange{v_y}=\norm{\orange{\vec{v}}}\cdot\sin\green{\theta}#, where #\norm{\orange{\vec{v}}}# is the magnitude of the velocity and #\green{\theta} # is its direction, as shown in Figure 2. Initial values are denoted with a subscript #0#, as usual.

Step 2 Treat the motion as two independent one-dimensional motions, one horizontal and the other vertical.
The equations of motion for horizontal and vertical motion take the following forms:

Horizontal motion
(#\purple{a_x} = \purple{0}#)

\[ \begin{array}{rcl}\blue{x} &=&\blue{{x}_{0}}+\orange{v_x}\cdot t \\
\orange{v_x}&=&\orange{v_{0x}}\;\,=\;\, \text{velocity is a constant}\end{array}\]

Vertical motion
(Assuming the positive direction is upwards)

\[\begin{array}{rcl}
\purple{a_y}&=&-\purple{g}\;\,=\;\, -\purple{\unit{9.81}{m/s^2}}\\
\blue{y} &=&\blue{{y}_{0}}+\dfrac{1}{2}\cdot (\orange{v_{0y}}+\blue{v_y})\cdot t\\
\orange{v_y}&=&\orange{v_{0y}}-\purple{g}\cdot t\\
\blue{y} &=&\blue{{y}_{0}}+\orange{v_{0y}}\cdot t-\dfrac{1}{2}\cdot {\purple{g}\cdot t}^{2}\\
\orange{v_y}^{2}&=&\orange{v_{0y}}^{2}-2\cdot \purple{g}\cdot (\blue{y}-\blue{{y}_{0}})\end{array}
\]

Step 3 Solve for the unknowns in the two separate motions, one horizontal and one vertical. Note that the only common variable between the motions is the time #t#. The problem-solving procedures here are the same as for one-dimensional motion and are illustrated in the solved examples below.

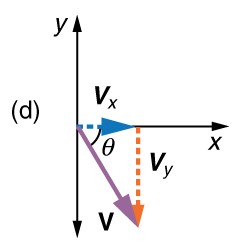
Step 4 Recombine the two motions to find the total displacement #\blue{\vec{s}}# and velocity #\orange{\vec{v}}#. Because the #x#- and #y#-motions are perpendicular, we determine these vectors by using the techniques outlined in the Vector addition and subtraction: analytical methods and employing both #\norm{A}=\sqrt{{A}_{x}^{2}+{A}_{y}^{2}}# and #\green{\theta} ={\tan}^{-1}({A}_{y}/{A}_{x})# in the following form, where #\green{\theta} # is the direction of the displacement #\blue{\vec{s}}# and #\green{\theta_v}# is the direction of the velocity #\orange{\vec{v}}#

Total displacement and velocity
\[ \begin{array}{rcl}
\blue{\norm{\vec{s}}}&=&\sqrt{\blue{x}^{2}+\blue{y}^{2}}\\
\green{\theta} &=&{\tan}^{-1}(\blue{y}/\blue{x})\\
\orange{\norm{\vec{v}}}&=&\sqrt{\orange{v_x}^{2}+\orange{v_y}^{2}}\\
\green{\theta_v}&=&{\tan}^{-1}(\orange{v_y}/\orange{v_x})
\end{array}
\]

Fig. 2 (a) We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. (b) The horizontal motion is simple, because #\purple{a_x}=\purple{0}# and #\orange{v_x}# is thus constant. (c) The velocity in the vertical direction begins to decrease as the object rises; at its highest point, the vertical velocity is zero. As the object falls towards the Earth again, the vertical velocity increases again in magnitude but points in the opposite direction to the initial vertical velocity. (d) The #x#- and #y#-motions are recombined to give the total velocity at any given point on the trajectory.

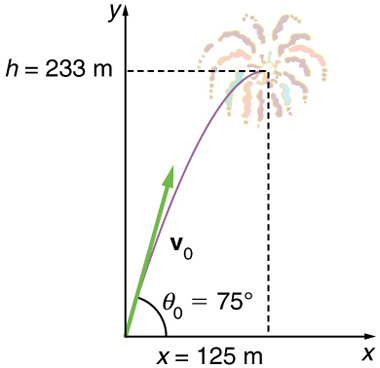
A fireworks projectile explodes high and away

During a fireworks display, a shell is shot into the air with an initial speed of #\orange{\unit{65.63}{m/s}}# at an angle of #\green{62.43^\circ}# above the horizontal, as illustrated in Figure 3. The fuse is timed to ignite the shell just as it reaches its highest point above the ground.

Calculate the height at which the shell explodes.

1. Outline a strategy

Because air resistance is negligible for the unexploded shell, the analysis method outlined above can be used. The motion can be broken into horizontal and vertical motions. In this case, we focus on the vertical motion, in which #\purple{a_y}=–\purple{g}#. We can then define #\blue{y_0}# to be zero and solve for the desired quantity.

2. Solve for the height

By “height” we mean the altitude or vertical position #\blue{y}# above the starting point. The highest point in any trajectory, called the apex, is reached when #\orange{v_y}=\orange{0}#. Since we know the initial and final velocities, as well as the initial position, we use the following equation to find #\blue{y}#
\[ \begin{array}{rcl}
\orange{v_y}^{2}&=&\orange{{v}}_\orange{0y}^2-2\cdot \purple{g}\cdot (\blue{y}-\blue{y_0})\\
&& \quad\blue{\text{time-independent equation of motion}}\\
\orange{0}&=&\orange{{v}}_\orange{0y}^2-2\cdot \purple{g}\cdot \blue{y}\\
&& \quad\blue{\text{replaced } y_0=0\text{ and } v_y = 0}\\
\blue{y}&=&\dfrac{\orange{{v}}_\orange{0y}^2}{2\cdot \purple{g}}\\
&& \quad\blue{\text{solved for }y}
\end{array} \]

Fig. 3 The trajectory of a fireworks shell. The fuse is set to explode the shell at the highest point in its trajectory, which, for the values shown in the figure, is found to be at a height of #\blue{\unit{233}{m}}# and #\blue{\unit{125}{m}}# away horizontally.

Now we must find #\orange{{v}_{0y}}#, the component of the initial velocity in the #y#-direction. It is given by #\orange{{v}_{0y}}=\orange{{v}_{0}}\cdot\sin\green{\theta} #, where #\orange{{v}_{0y}}# is the initial velocity of #\orange{\unit{65.63}{m/s}}#, and #\green{{\theta }_{0}}=\green{62.43^\circ}# is the initial angle

\[ \begin{array}{rcl}
\orange{{v}_{0y}}&=&\orange{{v}_{0}}\cdot\sin\green{{\theta }_{0}}\\
&& \quad\blue{y\text{-component of the initial velocity}}\\
&=&\orange{65.63}\cdot \sin (\green{62.43^\circ})\\
&& \quad\blue{\text{filled in numerical values}}\\
&=&\orange{\unit{58.18}{m/s}}\\
&& \quad\blue{\text{computed}}
\end{array}
\]

and #\blue{y}# is
\[ \begin{array}{rcl}
\blue{y}&=&\dfrac{\orange{{v}}_\orange{0y}^2}{2\cdot \purple{g}}\\
&& \quad\blue{\text{expression for }y}\\
&=&\dfrac{(\orange{58.18})^{2}}{2\cdot \purple{9.81} }\\
&& \quad\blue{\text{filled in numerical values}}\\
&=& \blue{\unit{172.5}{m}}\\
&& \quad\blue{\text{computed}}\\
&=& \blue{\unit{173}{m}}\\
&& \quad\blue{\text{expressed the result with three significant digits}}\\
\end{array}\]

Discussion

Because the positive direction is upwards, the initial velocity is positive, as is the maximum height, but the acceleration due to gravity is negative. Moreover, the maximum height depends only on the vertical component of the initial velocity, so that any projectile with a #\orange{\unit{58.18}{m/s}}# initial vertical component of velocity will reach a maximum height of #\blue{\unit{173}{m}}# (neglecting air resistance). The numbers in this example are reasonable for large fireworks displays, the shells of which do reach such heights before exploding. In practice, air resistance is not completely negligible, and so the initial velocity would have to be somewhat larger than that given to reach the same height.

New example