Physical quantities and units

[OpenStax, College physics 2e, Introduction: the nature of science and physics] The nature of science and physics: Physics: an introduction

Physical quantities and units

The range of objects and phenomena studied in physics is immense. From the incredibly short lifetime of an atomic nucleus to the age of the Earth, from the tiny sizes of sub-nuclear particles to the vast distance to the edges of the known universe, from the force exerted by a jumping flea to the force between Earth and the Sun, there are enough factors of #10# to challenge the imagination of even the most experienced scientist. Giving numerical values for physical quantities and equations for physical principles allows us to understand nature much more deeply than does qualitative description alone. To comprehend these vast ranges, we must also have accepted units in which to express them. And we shall find that (even in the potentially mundane discussion of #\blue{\text{meters}}#, #\green{\text{kilograms}}#, and #\orange{\text{seconds}}#) a profound simplicity of nature appears: all physical quantities can be expressed as combinations of only four fundamental physical quantities: length, mass, time, and electric current.

Physical quantity

We define a physical quantity either by specifying how it is measured or by stating how it is calculated from other measurements. For example, we define distance and time by specifying methods for measuring them, whereas we define average speed by stating that it is calculated as distance traveled divided by time of travel.

When we measure a physical quantity, we need to have something to express that measurement, which we do through units.

Units

Measurements of physical quantities are expressed in terms of units, which are standardized values. For example, the length of a race, which is a physical quantity, can be expressed in units of #\blue{\text{meters}}# (for sprinters) or kilometers (for distance runners). Without standardized units, it would be extremely difficult for scientists to express and compare measured values in a meaningful way. There are two major systems of units used in the world: SI units (also known as the metric system) and English units (also known as the customary or imperial system). We will only use the former throughout this text.

Table 1 gives the fundamental SI units that are used throughout this textbook.

Table 1 Fundamental SI units

Length	Mass	Time	Electric current
#\blue{\text{meter } (\unit{\hspace{-5 mu}}{m})}#	#\green{\text{kilogram }(\unit{\hspace{-5 mu}}{kg})}#	#\orange{\text{second } (\unit{\hspace{-5 mu}}{s})}#	ampere (#\unit{\hspace{-5 mu}}{A}#)

Systems of units

English units were historically used in nations once ruled by the British Empire and are still widely used in the United States. Virtually every other country in the world now uses SI units as the standard; the metric system is also the standard system agreed upon by scientists and mathematicians. The acronym “SI” is derived from the French Système International.

It is an intriguing fact that some physical quantities are more fundamental than others and that the most fundamental physical quantities can be defined only in terms of the procedure used to measure them.

Fundamental vs. derived units

The units in which those most fundamental physical quantities are measured are thus called fundamental units. In this textbook, the fundamental physical quantities are taken to be length, mass, time, and electric current. All other physical quantities, such as force and electric charge, can be expressed as algebraic combinations of length, mass, time, and current (for example, speed is length divided by time); these units are called derived units.

Nonstandard units

While there are numerous types of units that we are all familiar with, there are others that are much more obscure. For example, a firkin is a unit of volume that was once used to measure beer. One firkin equals about #34# liters. To learn more about nonstandard units, use a dictionary or encyclopedia to research different “weights and measures.” Take note of any unusual units, such as a barleycorn, that are not listed in the text. Think about how the unit is defined and state its relationship to SI units.

The quest for microscopic standards for basic units

The fundamental units described in this chapter are those that produce the greatest accuracy and precision in measurement. There is a sense among physicists that, because there is an underlying microscopic substructure to matter, it would be most satisfying to base our standards of measurement on microscopic objects and fundamental physical phenomena such as the speed of light. A microscopic standard has been accomplished for the standard of time, which is based on the oscillations of the cesium atom.

The standard for length was once based on the wavelength of light (a small-scale length) emitted by a certain type of atom, but it has been supplanted by the more precise measurement of the speed of light. If it becomes possible to measure the mass of atoms or a particular arrangement of atoms such as a silicon sphere to greater precision than the #\green{\text{kilogram}}# standard, it may become possible to base mass measurements on the small scale. There are also possibilities that electrical phenomena on the small scale may someday allow us to base a unit of charge on the charge of electrons and protons, but at present current and charge are related to large-scale currents and forces between wires.

Below, we discuss the units of time, length, and mass: respectively the #\orange{\text{second}}#, the #\blue{\text{meter}}#, and the #\green{\text{kilogram}}#.

The second, the meter, and the kilogram

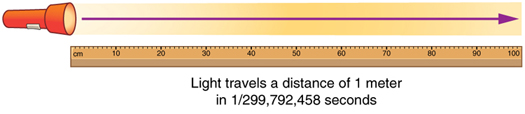
The SI units for time, length, and mass are, respectively, the second, the meter, and the kilogram. Over the years, their definitions have changed in order to make measurements of their associated quantities more accurate. For instance, the current definition of the #\orange{\text{second}}# makes reference to regular atomic vibrations, but it was not always like this. The reason for updating the definitions of these fundamental units is that all measurements are ultimately expressed in terms of fundamental units and can be no more accurate than are the fundamental units themselves.

On the expandable boxes below, you can find a brief history of the many definitions of the #\orange{\text{second}}#, the #\blue{\text{meter}}#, and the #\green{\text{kilogram}}#.

The second

The SI unit for time, the #\orange{\textbf{second}}# (abbreviated #\orange{\unit{\hspace{-5 mu}}{s}}#), has a long history. For many years it was defined as #1/8.6400\cdot 10^4# of a mean solar day. More recently, a new standard was adopted to gain greater accuracy and to define the #\orange{\text{second}}# in terms of a non-varying, or constant, physical phenomenon (because the solar day is getting longer due to very gradual slowing of the Earth’s rotation). Cesium atoms can be made to vibrate in a very steady way, and these vibrations can be readily observed and counted. In 1967 the #\orange{\text{second}}# was redefined as the time required for #9.192631770\cdot 10^9# of these vibrations (see Figure 1).

Fig. 1 An atomic clock such as this one uses the vibrations of cesium atoms to keep time to a precision of better than a microsecond per year. The fundamental unit of time, the #\orange{\text{second}}#, is based on such clocks. This image is looking down from the top of an atomic fountain nearly #\blue{9\text{ meters}}# tall! Credit: Steve Jurvetson/Flickr.

The meter

The SI unit for length is the #\blue{\textbf{meter}}# (abbreviated #\blue{\unit{\hspace{-5 mu}}{m}}#); its definition has also changed over time to become more accurate and precise. The #\blue{\text{meter}}# was first defined in 1791 as #1/10^7# of the distance from the equator to the North Pole. This measurement was improved in 1889 by redefining the #\blue{\text{meter}}# to be the distance between two engraved lines on a platinum-iridium bar now kept near Paris. By 1960, it had become possible to define the #\blue{\text{meter}}# even more accurately in terms of the wavelength of light, so it was again redefined as #1.65076373\cdot 10^6# wavelengths of orange light emitted by krypton atoms. In 1983, the #\blue{\text{meter}}# was given its present definition (partly for greater accuracy) as the distance light travels in a vacuum in #1/2.99792458\cdot 10^8# of a #\orange{\text{second}}# (see Figure 2). This change defines the speed of light to be exactly #2.99792458\cdot 10^8# meters per second. The length of the #\blue{\text{meter}}# will change if the speed of light is someday measured with greater accuracy.

Fig. 2 The #\blue{\text{meter}}# is defined to be the distance light travels in #1/299\,792\,458# of a #\orange{\text{second}}# in a vacuum. Distance traveled is speed multiplied by time.

The kilogram

The SI unit for mass is the #\green{\textbf{kilogram}}# (abbreviated #\green{\unit{\hspace{-5 mu}}{kg}}#); it was previously defined to be the mass of a platinum-iridium cylinder kept with the old #\blue{\text{meter}}# standard at the International Bureau of Weights and Measures near Paris. Exact replicas of the previously defined #\green{\text{kilogram}}# are also kept at the United States National Institute of Standards and Technology, or NIST, located in Gaithersburg, Maryland, outside of Washington D.C., and at other locations around the world. The determination of all other masses could be ultimately traced to a comparison with the standard mass. Even though the platinum-iridium cylinder was resistant to corrosion, airborne contaminants were able to adhere to its surface, slightly changing its mass over time. In May 2019, the scientific community adopted a more stable definition of the #\green{\text{kilogram}}#. The #\green{\text{kilogram}}# is now defined in terms of the #\orange{\text{second}}#, the #\blue{\text{meter}}#, and Planck's constant, #h# (a quantum mechanical value that relates a photon's energy to its frequency).

Electric current and its accompanying unit, the ampere, will not be discussed at this point in the course, as the initial modules are only concerned with mechanics, fluids, heat, and waves. In these subjects all pertinent physical quantities can be expressed in terms of the fundamental units of length, mass, and time.

Let us now discuss the metric system.

The metric system

SI units are part of the metric system. The metric system is convenient for scientific and engineering calculations because the units are categorized by factors of #10#. Table 2 gives metric prefixes and symbols used to denote various factors of #10#.

Metric systems have the advantage that conversions of units involve only powers of #10#. There are #100# centimeters in a #\blue{\text{meter}}#, #\blue{1000 \text{ meters}}# in a kilometer, and so on. In nonmetric systems, such as the system of U.S. customary units, the relationships are not as simple; for instance, there are #12# inches in a foot, #5280# feet in a mile, and so on. Another advantage of the metric system is that the same unit can be used over extremely large ranges of values simply by using an appropriate metric prefix. For example, distances in #\blue{\text{meters}}# are suitable in construction, while distances in kilometers are appropriate for air travel, and the tiny measure of nanometers are convenient in optical design. With the metric system there is no need to invent new units for particular applications.

The powers of #10# discussed above not only make conversions simpler and uniform, but also lead to the very important concept of order of magnitude.

Orders of magnitude

The term order of magnitude refers to the scale of a value expressed in the metric system. Each power of #10# in the metric system represents a different order of magnitude. For example, #{10}^{1}#, #{10}^{2}#, #{10}^{3}#, and so forth are all different orders of magnitude. All quantities that can be expressed as a product of a specific power of #10# are said to be of the same order of magnitude. For example, the number #800# can be written as #8\cdot {10}^{2}#, and the number #450# can be written as #4.5\cdot{10}^{2}#. Thus, the numbers #800# and #450# are of the same order of magnitude: #{10}^{2}#. Order of magnitude can be thought of as a ballpark estimate for the scale of a value. The diameter of an atom is on the order of #\blue{\unit{{10}^{-9}}{ m}}#, while the diameter of the Sun is on the order of #\blue{\unit{{10}^{9}}{m}}#.

At the end of the page you can find Table 3, containing the prefixes for different powers of #10#, their symbols, and some examples of those orders of magnitude.

It is often necessary to convert from one type of unit to another. For example, if you are reading a European cookbook, some quantities may be expressed in units of liters and you need to convert them to cups. Or, perhaps you are reading walking directions from one location to another and you are interested in how many kilometers you will be walking. In this case, you might need to convert units of #\blue{\text{meters}}# to kilometers.

Unit conversion and dimensional analysis

Let us consider a simple example of how to convert units. Let us say that we want to convert #\blue{80\text{ meters}}# (#\unit{\hspace{-5 mu}}{\blue{m}}#) to kilometers (#\unit{\hspace{-5 mu}}{km}#).

The first thing to do is to list the units that you have and the units that you want to convert to. In this case, we have units in #\blue{\text{meters}}# and we want to convert to kilometers.

Next, we need to determine a conversion factor relating #\blue{\text{meters}}# to kilometers. A conversion factor is a ratio expressing how many of one unit are equal to another unit. For example, there are #100# centimeters in #\blue{1 \text{ meter}}#, #12# inches in #1# foot, #\orange{60 \text{ seconds}}# in #1# minute, and so on. In this case, we know that there are #\blue{1000 \text{ meters}}# in #1# kilometer.

Now we can set up our unit conversion. We will write the units that we have and then multiply them by the conversion factor so that the units cancel out, as shown:

\[ \begin{array}{rcl}\blue{\unit{80}{m}}\cdot\dfrac{\unit{1}{km}}{\blue{\unit{1000}{m}}}&=&\unit{0.080}{km}\end{array} \]

Note that the unwanted#\blue{\unit{}{m}}# unit cancels, leaving only the desired #\unit{\!}{km}# unit. You can use this method to convert between any types of unit.

The tab below gives an impression of the vast range of scales in which physics applies.

Scale of physics

The vastness of the universe and the breadth over which physics applies are illustrated by the wide range of examples of known lengths, masses, and times in Table 2. Examination of this table will give you some feeling for the range of possible topics and numerical values (see also Figure 3 and Figure 4).

Fig. 3 Tiny phytoplankton swims among crystals of ice in the Antarctic Sea. They range from a few micrometers to as much as #2# millimeters in length. Credit: Prof. Gordon T. Taylor, Stony Brook University; NOAA Corps Collections.

Fig. 4 Galaxies collide #2.4# billion light years away from Earth. The tremendous range of observable phenomena in nature challenges the imagination. Credit: NASA/CXC/UVic./A. Mahdavi et al. Optical/lensing: CFHT/UVic./H. Hoekstra et al.

Table 2 Approximate values of length, mass, and time

Lengths in meters		Masses in kilograms (more precise values in parentheses)		Times in seconds (more precise values in parentheses)
#{10}^{-18}#	Present experimental limit to smallest observable detail	#{10}^{-30}#	Mass of an electron #(\unit{9.11\cdot{10}^{-31}}{kg})#	#{10}^{-23}#	Time for light to cross a proton
#{10}^{-15}#	Diameter of a proton	#{10}^{-27}#	Mass of a hydrogen atom #(\unit{1.67\cdot{10}^{-27}}{kg})#	#{10}^{-22}#	Mean life of an extremely unstable nucleus
#{10}^{-14}#	Diameter of a uranium nucleus	#{10}^{-15}#	Mass of a bacterium	#{10}^{-15}#	Time for one oscillation of visible light
#{10}^{-10}#	Diameter of a hydrogen atom	#{10}^{-5}#	Mass of a mosquito	#{10}^{-13}#	Time for one vibration of an atom in a solid
#{10}^{-8}#	Thickness of membranes in cells of living organisms	#{10}^{-2}#	Mass of a hummingbird	#{10}^{-8}#	Time for one oscillation of an FM radio wave
#{10}^{-6}#	Wavelength of visible light	#1#	Mass of a liter of water (about a quart)	#{10}^{-3}#	Duration of a nerve impulse
#{10}^{-3}#	Size of a grain of sand	#{10}^{2}#	Mass of a person	#1#	Time for one heartbeat
#1#	Height of a 4-year-old child	#{10}^{3}#	Mass of a car	#{10}^{5}#	One day #(\unit{8.64\cdot{10}^{4}}{s})#
#{10}^{2}#	Length of a football field	#{10}^{8}#	Mass of a large ship	#{10}^{7}#	One year (y) #(\unit{3.16\cdot{10}^{7}}{s})#
#{10}^{4}#	Greatest ocean depth	#{10}^{12}#	Mass of a large iceberg	#{10}^{9}#	About half the life expectancy of a human
#{10}^{7}#	Diameter of the Earth	#{10}^{15}#	Mass of the nucleus of a comet	#{10}^{11}#	Recorded history
#{10}^{11}#	Distance from the Earth to the Sun	#{10}^{23}#	Mass of the Moon #(\unit{7.35\cdot {10}^{22}}{kg})#	#{10}^{17}#	Age of the Earth
#{10}^{16}#	Distance traveled by light in 1 year (a light year)	#{10}^{25}#	Mass of the Earth #(\unit{5.97\cdot{10}^{24}}{kg})#	#{10}^{18}#	Age of the universe
#{10}^{21}#	Diameter of the Milky Way galaxy	#{10}^{30}#	Mass of the Sun #(\unit{1.99\cdot{10}^{30}}{kg})#
#{10}^{22}#	Distance from the Earth to the nearest large galaxy (Andromeda)	#{10}^{42}#	Mass of the Milky Way galaxy (current upper limit)
#{10}^{26}#	Distance from the Earth to the edges of the known universe	#{10}^{53}#	Mass of the known universe (current upper limit)

Next, you can find an example of unit conversion in a problem. Below that, you can find a table with all the metric prefixes, their values, and some examples of their use.

Unit conversions: a short drive home

Suppose you drive the #\unit{10.0}{km}# from your university to home in #\unit{20.0}{min}#. Calculate your average speed (a) in kilometers per hour (#\unit{\hspace{-5 mu}}{km/h}#) and (b) in meters per second (#\unit{\hspace{-5 mu}}{\blue{m}/\orange{s}}#).

Note: average speed is distance traveled divided by time of travel.

1. Outline a strategy

First we calculate the average speed using the given units. Then we can get the average speed into the desired units by picking the correct conversion factor and multiplying by it. The correct conversion factor is the one that cancels the unwanted unit and leaves the desired unit in its place.

2. Solve for speed (a)

Calculate average speed. Average speed is distance traveled divided by time of travel. Take this definition as a given for now, average speed and other motion concepts will be covered in a later module. In equation form this definition reads
\[ \text{average speed} =\dfrac{\text{distance}}{\text{time}}\]
Substitute the given values for distance and time.
\[ \text{average speed} =\dfrac{\unit{10.0}{km}}{\unit{20.0}{min}}=\unit{0.500}{km/min}\]
Convert#\unit{}{km/min}# to#\unit{}{km/h}#: multiply by the conversion factor that will cancel minutes and leave hours. There are #60# minutes in each #1# hour. The conversion factor is therefore
\[\dfrac{\unit{60}{min}}{\unit{1}{h}} = \unit{60}{\dfrac{min}{h}}\] which we can use to obtain the answer
\[ \begin{array}{rcl}\text{average speed} &=& \unit{0.500}{\dfrac{km}{min}}\cdot \unit{60}{\dfrac{min}{h}}\\ &=&\unit{30.0}{\dfrac{km}{h}}\end{array}\]

Discussion

To check your answer, consider the following steps.

Be sure that you have properly canceled the units in the unit conversion. If you have written the unit conversion factor the other way around, the units will not cancel properly in the equation; rather, they will give you the wrong units as follows:
\[\dfrac{\unit{\!}{ km}}{\unit{\!}{min}}\cdot \dfrac{\unit{1}{ h}}{\unit{60}{ min}}=\dfrac{1}{60}\dfrac{\unit{\!}{ km\cdot h}}{\unit{\!}{ min^2}} \]
which are obviously not the desired units of#\unit{}{km/h}#.
Check that the units of the final answer are the desired units. The problem asked us to solve for average speed in units of #\unit{\!}{km/h}# and we have indeed obtained these units.
Check the significant figures. Because each of the values given in the problem has three significant figures, the answer should also have three significant figures. The answer #\unit{30.0}{km/h}# does indeed have three significant figures, so this is appropriate. Note that the significant figures in the conversion factor are not relevant because an hour is defined to be #60# minutes, so the precision of the conversion factor is perfect.
Next, check whether the answer is reasonable. Let us consider some information from the problem: if you travel #\unit{10}{km}# in a third of an hour (#\unit{20}{min}#), you would travel three times that far in an hour. The answer does seem reasonable.

3. Convert units (b)

There are several ways to convert the average speed into meters per second.

Start with the answer to (a) and convert #\unit{\!}{km/h}# to #\unit{\!}{\blue{m}/\orange{s}}#. Two conversion factors are needed: one to convert hours to seconds, and another to convert kilometers to meters. Every #1# hour consists of #3600# seconds and there are #1000# meters in each #1# kilometer. The resulting conversion factors are therefore: \[ \dfrac{\unit{1}{h}}{\orange{\unit{3600}{s}}} \qquad \text{and} \qquad \dfrac{\blue{\unit{1000}{m}}}{\unit{1}{km}}\]
Multiplying by these yields
\[ \begin{array}{rcl}\text{Average speed}&=&\unit{30.0}{\dfrac{ km}{ h}} \cdot \dfrac{\unit{1}{ h}}{\orange{\unit{3600}{s}}} \cdot \dfrac{\blue{\unit{1000}{ m}}}{\unit{1}{km}}\\ &=& \unit{8.33}{\dfrac{\blue{m}}{\orange{s}}}\end{array}\]

Discussion

If we had started with #\unit{0.500}{km/min}#, we would have needed different conversion factors, but the answer would have been the same: #\unit{8.33}{\blue{m}/\orange{s}}#.

New example

Table 3 Metric prefixes for powers of 10 and their symbols

Prefix	Symbol	Value	Example (some are approximate)
exa	E	#{10}^{18}#	exameter	Em	#\unit{{10}^{18}}{m}#	distance light travels in a century
peta	P	#{10}^{15}#	petasecond	Ps	#\unit{{10}^{15}}{s}#	30 million years
tera	T	#{10}^{12}#	terawatt	TW	#\unit{{10}^{12}}{W}#	powerful laser output
giga	G	#{10}^{9}#	gigahertz	GHz	#\unit{{10}^{9}}{Hz}#	a microwave frequency
mega	M	#{10}^{6}#	megacurie	MCi	#\unit{{10}^{6}}{Ci}#	high radioactivity
kilo	k	#{10}^{3}#	kilometer	km	#\unit{{10}^{3}}{m}#	about 6/10 mile
hecto	h	#{10}^{2}#	hectoliter	hL	#\unit{{10}^{2}}{L}#	26 gallons
deka	da	#{10}^{1}#	dekagram	dag	#\unit{{10}^{1}}{g}#	teaspoon of butter
—	—	#{10}^{0}# (=1)
deci	d	#{10}^{-1}#	deciliter	dL	#\unit{{10}^{-1}}{L}#	less than half a soda
centi	c	#{10}^{-2}#	centimeter	cm	#\unit{{10}^{-2}}{m}#	fingertip thickness
milli	m	#{10}^{-3}#	millimeter	mm	#\unit{{10}^{-3}}{m}#	flea at its shoulders
micro	µ	#{10}^{-6}#	micrometer	µm	#\unit{{10}^{-6}}{m}#	detail in microscope
nano	n	#{10}^{-9}#	nanogram	ng	#\unit{{10}^{-9}}{g}#	small speck of dust
pico	p	#{10}^{-12}#	picofarad	pF	#\unit{{10}^{-12}}{F}#	small capacitor in radio
femto	f	#{10}^{-15}#	femtometer	fm	#\unit{{10}^{-15}}{m}#	size of a proton
atto	a	#{10}^{-18}#	attosecond	as	#\unit{{10}^{-18}}{s}#	time light crosses an atom