Newton’s second law of motion: concept of a system

[Openstax, College physics 2e, Dynamics: Force and Newton's laws of motion] Force and Newton's laws of motion: Newton's laws

Newton’s second law of motion: concept of a system

Newton’s second law of motion is closely related to Newton’s first law of motion. It mathematically states the cause-and-effect relationship between force and changes in motion. Newton’s second law of motion is more quantitative and is used extensively to calculate what happens in situations involving a force. Before we can write down Newton’s second law as a simple equation giving the exact relationship of force, mass, and acceleration, we need to sharpen some ideas that have already been mentioned.

First, what do we mean by a change in motion? The answer is that a change in motion is equivalent to a change in velocity. A change in velocity means, by definition, that there is an acceleration. Newton’s first law says that a net external force causes a change in motion; thus, we see that a net external force causes acceleration.

External vs. internal force
Another question immediately arises. What do we mean by an external force? An intuitive notion of external is correct: an external force acts from outside the system of interest. For example, in Figure 1 (a), the system of interest is the wagon plus the child in it. The two forces exerted by the other children are external forces. An internal force acts between elements of the system. Again, looking at Figure 1 (a), the force the child in the wagon exerts to hang onto the wagon is an internal force between elements of the system of interest. Only external forces affect the motion of a system, according to Newton’s first law (the internal forces actually cancel, as we shall see in the next section). You must define the boundaries of the system before you can determine which forces are external. Sometimes, the system is obvious, whereas other times, identifying the boundaries of a system is more subtle. The concept of a system is fundamental to many areas of physics, as is the correct application of Newton’s laws. This concept will be revisited many times on our journey through physics.

Fig. 1 Different forces exerted on the same mass produce different accelerations. (a) Two children push a wagon with a child in it. Arrows representing all external forces are shown. The system of interest is the wagon and its rider. The weight #\vec{W}# of the system and the support of the ground #\vec{N}# (called the normal reaction) are also shown for completeness and are assumed to cancel. The vector #\vec{f}# represents the friction acting on the wagon, and it acts to the left, opposing the motion of the wagon. (b) All of the external forces acting on the system add together to produce a net force, #{\vec{F}}_{\text{net}}#. The free-body diagram shows all of the forces acting on the system of interest. The dot represents the center of mass of the system. Each force vector extends from this dot. Because two forces are acting to the right, we draw the vectors collinearly. (c) A larger net external force produces a larger acceleration ( #\vec{a}'>\vec{a}# ) when an adult pushes the child.

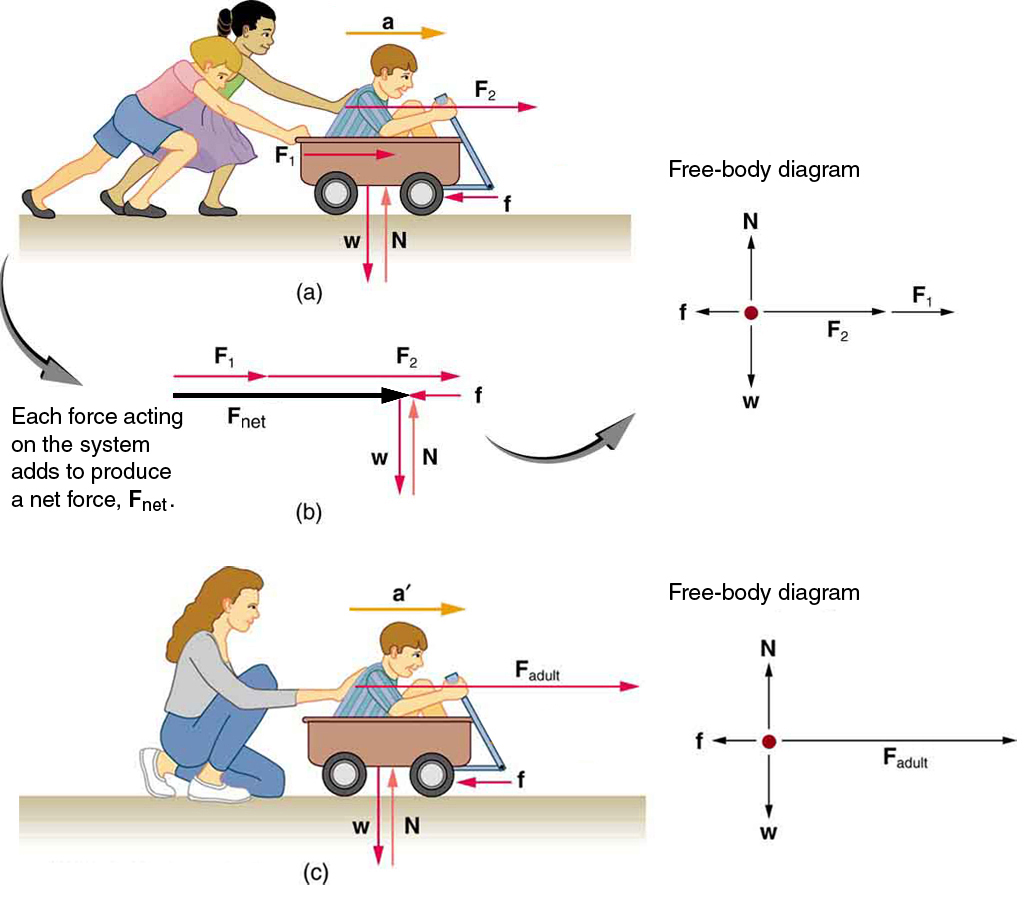
Now, it seems reasonable that acceleration should be directly proportional to and in the same direction as the net (total) external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure 1. In part (a), a smaller force causes a smaller acceleration than the larger force illustrated in part (c). For completeness, the vertical forces are also shown; they are assumed to cancel since there is no acceleration in the vertical direction. The vertical forces are the weight #\vec{W}# and the support of the ground #\vec{N}# (called the normal reaction), and the horizontal force #\vec{f}# represents the force of friction. These will be discussed in more detail in later pages. For now, we will define friction as a force that opposes the motion past each other of objects that are touching. Figure 1 (b) shows how vectors representing the external forces add together to produce a net force, #{\vec{F}}_{\text{net}}#.

Acceleration and net external force
To obtain an equation for Newton’s second law, we first write the relationship of acceleration and net external force as the proportionality

\[\blue{\vec{a}}\propto \green{{\vec{F}}_{\text{net}}}\]

where the symbol #\propto # means “proportional to”, and #\green{{\vec{F}}_{\text{net}}}# is the #\green{\mathbf{\text{net external force}}}#. The net external force is the vector sum of all external forces and can be determined graphically, using the head-to-tail method, or analytically, using components. The techniques are the same as for the addition of other vectors, and are covered in Vector addition and subtraction: graphical methods and Vector addition and subtraction: analytical methods. This proportionality states what we have said: acceleration is directly proportional to the net external force. Once the system of interest is chosen, it is important to identify the external forces and ignore the internal ones.

It is a tremendous simplification not to have to consider the numerous internal forces acting between objects within the system, such as muscular forces within the child’s body, let alone the myriad of forces between atoms in the objects, but by doing so, we can easily solve some very complex problems with only minimal error due to our simplification

The acceleration of an object is inversely proportional to its mass.

Acceleration and mass
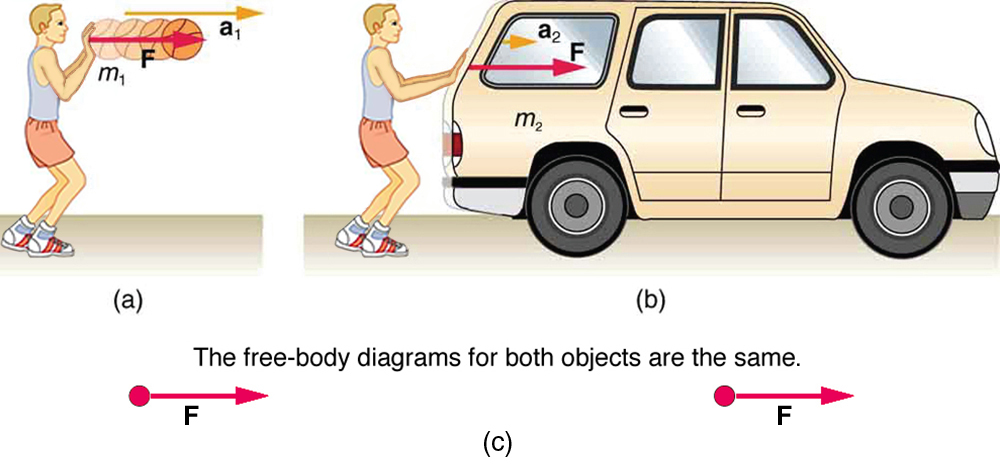
Now, it also seems reasonable that acceleration should be inversely proportional to the mass of the system. In other words, the larger the mass (the inertia), the smaller the acceleration produced by a given force. And indeed, as illustrated in Figure 2, the same net external force applied to a car produces a much smaller acceleration than when applied to a basketball. The proportionality is written as

\[\blue{\vec{a}}\propto \dfrac{1}{\orange{m}}\]

where #\orange{m}# is the mass of the system. Experiments have shown that acceleration is exactly inversely proportional to mass, just as it is exactly linearly proportional to the net external force.

Fig. 2 The same force exerted on systems of different masses produces different accelerations. (a) A basketball player pushes on a basketball to make a pass (the effect of gravity on the ball is ignored). (b) The same player exerts an identical force on a stalled SUV and produces a far smaller acceleration (even if friction is negligible). (c) The free-body diagrams are identical, permitting a direct comparison of the two situations. A series of patterns for the free-body diagram will emerge as you do more problems.

It has been found that the acceleration of an object depends only on the net external force and the mass of the object. Combining the two proportionalities just given yields Newton's second law of motion.

Newton’s second law of motion

The acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system and inversely proportional to its mass. In equation form, Newton’s second law of motion is

\[ \blue{\vec{a}} = \dfrac{\green{\vec{F}_{\text{net}}}}{\orange{m}} \]

This is often written in the more familiar form

\[\green{\vec{F}_{\text{net}}}= \orange{m}\cdot \blue{\vec{a}}\]

When only the magnitude of force and acceleration are considered, this equation is simply

\[\green{\norm{\vec{F}_{\text{net}}}}= \orange{m}\cdot \blue{\norm{\vec{a}}}\]

Although these last two equations are really the same, the first gives more insight into what Newton’s second law means. The law is a cause-and-effect relationship among three quantities that is not simply based on their definitions. The validity of the second law is completely based on experimental verification.

Newton's second law is used to define the units of force in terms of the three basic units for mass, length, and time.

Units of force
The SI unit of force is called the newton (abbreviated #\unit{\!}{N}#) and is the force needed to accelerate a #\unit{1}{kg}# system at the rate of #\unit{1}{m/s^{2}}#. That is, since #\green{\vec{F}_{\text{net}}}= \orange{m}\cdot \blue{\vec{a}}#,

\[ \unit{1}{N} = \unit{1}{kg}\cdot \unit{\!}{m/s^{2}}\]

Other units
While almost the entire world uses the newton for the unit of force, in the United States, the most familiar unit of force is the pound (#\unit{\!}{lb}#), where #\unit{1}{N}=\unit{0.225}{lb}#. Despite having the same name, the unit of force pound should not be confused with the unit of mass pound, which corresponds to #\unit{0.454}{kg}#.

Weight and the gravitational force

When an object is dropped, it accelerates toward the center of Earth. Newton’s second law states that a net force on an object is responsible for its acceleration. If air resistance is negligible, the net force on a falling object is the gravitational force, commonly called its #\green{\mathbf{\text{weight}}}#, #\green{\vec{W}}#. Weight can be denoted as a vector #\green{\vec{W}}# because it has a direction; down is, by definition, the direction of gravity. Hence, weight is a downward force. The magnitude of weight is denoted as #\green{\norm{\vec{W}}}#. Galileo was instrumental in showing that, in the absence of air resistance, all objects fall with the same acceleration #g#. Using Galileo’s result and Newton’s second law, we can derive an equation for weight.

Consider an object with mass #\orange{m}# falling downward toward Earth. It experiences only the downward force of gravity, which has magnitude #\green{\norm{\vec{W}}}#. Newton’s second law states that the magnitude of the net external force on an object is #\green{\norm{\vec{F}_{\text{net}}}}= \orange{m}\cdot \blue{\norm{\vec{a}}}#. Since the object experiences only the downward force of gravity, #\green{\norm{\vec{F}_{\text{net}}}}=\green{\norm{\vec{W}}}#. We know that the acceleration of an object due to gravity is #g#, or #\blue{\norm{\vec{a}}}=\blue{g}#. Substituting these into Newton’s second law gives us an equation for the weight.

Weight

This is the equation for weight, the magnitude of gravitational force on a mass #\orange{m}#,

\[\green{\norm{\vec{W}}}= \orange{m} \cdot \blue{g}\]

Since #\blue{g}= \blue{\unit{9.81}{m/s^2}}# on Earth, the weight of a #\orange{\unit{1.00}{kg}}# object on Earth is #\green{\unit{9.81}{N}}#, as we see,

\[\green{\norm{\vec{W}}}= \orange{m} \cdot \blue{g} = \orange{\unit{1.0}{kg}}\cdot \blue{\unit{9.81}{m/s^2}} = \green{\unit{9.81}{N}}\]
Recall that #g# can take a positive or negative value, depending on the positive direction in the coordinate system. Be sure to take this into consideration when solving problems with weight.

Free-fallWhen the net external force on an object is its weight, we say that it is in free-fall. That is, the only force acting on the object is the force of gravity. In the real world, when objects fall downward toward Earth, they are never truly in free-fall because there is always some upward force from the air acting on the object.

Broad definition of weight
The acceleration due to gravity #g# varies slightly over the surface of Earth so that the weight of an object depends on location and is not an intrinsic property of the object. Weight varies dramatically if one leaves Earth’s surface. On the Moon, for example, the acceleration due to gravity is only #\unit{1.62}{m/s^{2}}#. A #\unit{1.00}{kg}# mass thus has a weight of #\unit{9.81}{N}# on Earth and only about #\unit{1.62}{N}# on the Moon.

The broadest definition of weight in this sense is that the weight of an object is the gravitational force on it from the nearest large body, such as Earth, the Moon, the Sun, and so on. This is the most common and useful definition of weight in physics. It differs dramatically, however, from the definition of weight used by NASA and the popular media in relation to space travel and exploration. When they speak of “weightlessness” and “microgravity,” they are really referring to the phenomenon we call “free-fall” in physics. We shall use the above definition of weight, and we will make careful distinctions between free-fall and actual weightlessness.

Mass and weight are often used interchangeably in everyday language.

Common misconceptions: mass vs. weight

In science, these terms are distinctly different from one another. Mass is a measure of how much matter is in an object. The typical measure of mass is the kilogram. On the other hand, weight is a measure of the force of gravity acting on an object. Weight is equal to the mass of an object (#m#) multiplied by the acceleration due to gravity (#g#). Like any other force, weight is measured in terms of newtons.

Assuming the mass of an object is kept intact, it will remain the same, regardless of its location. However, because weight depends on the acceleration due to gravity, the weight of an object can change when the object enters into a region with stronger or weaker gravity. For example, the acceleration due to gravity on the Moon is #\unit{1.62}{m/s^{2}}# (which is much less than the acceleration due to gravity on Earth, #\unit{9.81}{m/s^{2}}#). If you measured your weight on Earth and then measured your weight on the Moon, you would find that you “weigh” much less, even though you do not look any skinnier. This is because the force of gravity is weaker on the Moon. In fact, when people say that they are “losing weight,” they really mean that they are losing “mass” (which in turn causes them to weigh less).

It is possible to perform a home experiment to better understand weight.

Take-Home Experiment: Mass and Weight

What do bathroom scales measure? When you stand on a bathroom scale, what happens to the scale? It depresses slightly. The scale contains springs that compress in proportion to your weight, similar to rubber bands that expand when pulled. The springs provide a measure of your weight (for an object that is not accelerating). This is a force in newtons (or pounds). In most countries, the measurement is divided by #9.81# to give a reading in mass units of kilograms. The scale measures weight but is calibrated to provide information about mass. While standing on a bathroom scale, push down on a table next to you. What happens to the reading? Why? Would your scale measure the same “mass” on Earth as on the Moon?

What acceleration can a person produce when pushing a lawn mower?

Suppose that the net external force (push minus friction) exerted on a lawn mower is #\green{\unit{49.2}{N}}# parallel to the ground. The mass of the mower is #\orange{\unit{20.9}{kg}}#. What is its acceleration?

Fig. 3 The net force on a lawn mower is #\green{\unit{49.2}{N}}# to the right. At what rate does the lawn mower accelerate to the right?

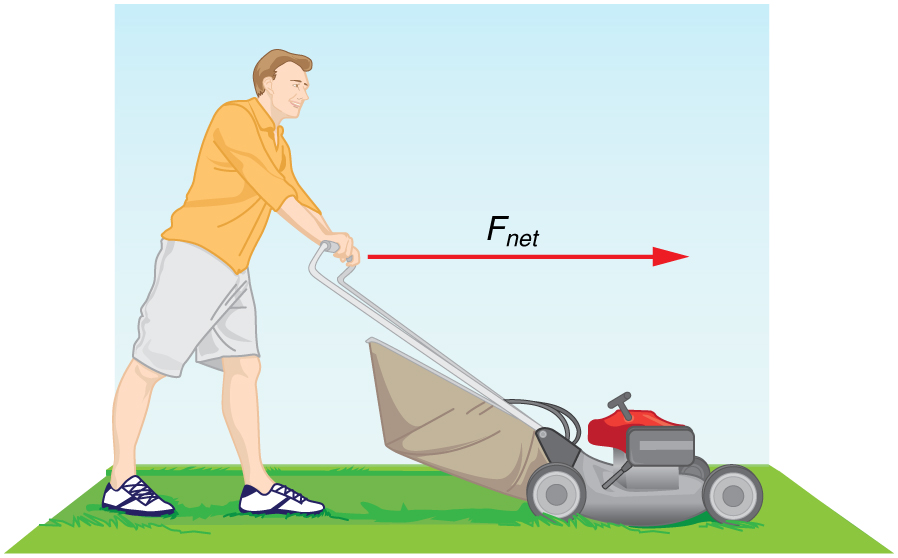
1. Outline a strategy

Since #\green{\vec{F}_{\text{net}}}# and #\orange{m}# are given, the acceleration can be calculated directly from Newton’s second law as stated in #\green{\vec{F}_{\text{net}}}= \orange{m}\cdot \blue{\vec{a}}#.

2. Solve for the acceleration

The magnitude of the acceleration #\blue{\norm{\vec{a}}}# is
\[ \begin{array}{rcl}
\blue{\norm{\vec{a}}} &=& \dfrac{\green{\norm{\vec{F}_{\text{net}}}}}{\orange{m}}\\
&& \quad\blue{\text{formula for the acceleration}}\\
&=& \dfrac{\green{49.2}}{\orange{20.9}}\\
&& \quad\blue{\text{filled in numerical values}}\\
&=& \blue{\unit{2.35}{m/s^2}}\\
&& \quad\blue{\text{computed}}
\end{array}\]
The units were obtained using
\[ \dfrac{\unit{1}{N}}{\unit{1}{kg}} = \dfrac{\unit{1}{kg}\cdot \unit{1}{m/s^{2}}}{\unit{1}{kg}} = \unit{1}{m/s^{2}}\]

Discussion

The direction of the acceleration is the same direction as that of the net force, which is parallel to the ground. There is no information given in this example about the individual external forces acting on the system, but we can say something about their relative magnitudes. For example, the force exerted by the person pushing the mower must be greater than the friction opposing the motion (since we know the mower moves forward), and the vertical forces must cancel if there is to be no acceleration in the vertical direction (the mower is moving only horizontally). The acceleration found is small enough to be reasonable for a person pushing a mower. Such an effort would not last too long because the person’s top speed would soon be reached.

New example