Inproducten op reële vectorruimten

Inproductruimten: Inproduct, lengte en hoek

Inproducten op reële vectorruimten

Om een indicatie te geven waar het begrip inproduct vandaan komt, kijken we in het vlak.

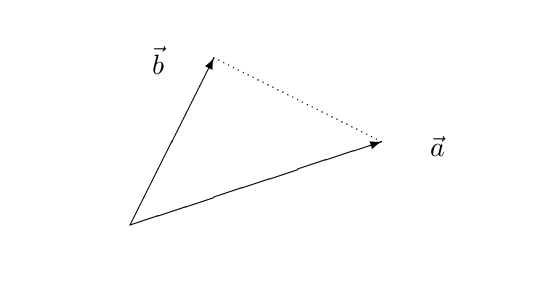
In een driehoek in het vlak waarvan twee zijden corresponderen met de vectoren $\vec{a}$ en $\vec{b}$ heeft de derde zijde lengte $\norm{\vec{a}-\vec{b}}$ . Als de hoek tussen de vectoren $\vec{a}$ en $\vec{b}$ gelijk is aan $\varphi$ , dan leert de cosinusregel dat
$\norm{\vec{a}-\vec{b}}^2 =\norm{\vec{a}}^2 + \norm{\vec{b}}^2 -2\,\norm{\vec{a}}\cdot\norm{\vec{b}}\cdot \cos(\varphi)$ De term $\norm{\vec{a}}\cdot\norm{\vec{b}}\cdot\cos(\varphi)$ in het rechter lid is het inproduct van twee vectoren $\vec{a}$ en $\vec{b}$ in het platte vlak. Door bijvoorbeeld $\vec{a}=\vec{b}$ te kiezen vinden we het kwadraat van de lengte van $\vec{a}$ terug. De hoek tussen twee vectoren is tevens ingebouwd in dit inproduct. Bij de theorie van inproducten in abstracte vectorruimten kunnen we niet met zo'n expliciete formule beginnen. We hebben ook geen norm gedefiniëerd, dus de uitdrukking hierboven zegt niets. Daarom gaan we uit van bepaalde eigenschappen die dit inproduct in het vlak blijkt te hebben: symmetrie in de twee argumenten $\vec{a}$ en $\vec{b}$ , lineariteit in elk van de argumenten $\vec{a}$ en $\vec{b}$ afzonderlijk en positiviteit van de uitdrukking als $\vec{a}=\vec{b}\ne\vec{0}$ . We definiëren aan de hand hiervan een inproduct op abstracte vectorruimten.

Laat $V$ een reële vectorruimte zijn. Een inproduct op $V$ is een functie die aan ieder tweetal vectoren $\vec{a},\vec{b}$ uit $V$ een reëel getal $\dotprod{\vec{a}}{\vec{b}}$ toevoegt zodanig dat aan de volgende drie eigenschappen voldaan is.

bilineariteit: $\dotprod{\vec{a}}{\vec{b}}$ is lineair in zowel $\vec{a}$ als $\vec{b}$ :
$\begin{array}{rcl} \dotprod{(\lambda \vec{v}+\mu \vec{w})}{\vec{b}}&= &\lambda \cdot(\dotprod{\vec{v}}{\vec{b}})+\mu\cdot (\dotprod{\vec{w}}{\vec{b}})\\ \dotprod{\vec{a} }{(\lambda \vec{v}+\mu \vec{w})} & =&\lambda\cdot (\dotprod{\vec{a}}{ \vec{v}})+\mu \cdot(\dotprod{\vec{a}}{\vec{w}}) \end{array}$ voor alle scalairen en vectoren;
symmetrie: $\dotprod{\vec{a}}{\vec{b}} = \dotprod{\vec{b}}{\vec{a}}$ voor alle $\vec{a},\vec{b}\in V$ ;
positief-definietheid: $\dotprod{\vec{a}}{\vec{a}}\geq 0$ voor alle $\vec{a}\in V$ , en $\dotprod{\vec{a}}{\vec{a}} = 0$ dan en slechts dan als $\vec{a}= \vec{0}$ .

Een reële vectorruimte met een inproduct wordt vaak een (reële) inproductruimte genoemd.

Een inproduct noemt men ook wel inwendig product. In het Engels wordt vaak de door de notatie $\dotprod{\vec{a}}{\vec{b}}$ gesuggereerde naam dot product gebruikt.

Complexe gevalHet inproduct in complexe vectorruimten wordt iets anders gedefinieerd. Dit wordt elders behandeld.

We kunnen in $\mathbb{R}^n$ op vele manieren een inproduct definiëren. Verreweg het meest gebruikt wordt het volgende inproduct dat we het standaardinproduct zullen noemen:
als $\vec{a}\ = \rv{a_1,a_2,\ldots,a_n}$ en $\vec{b}\ = \rv{b_1,b_2,\ldots,b_n}$ vectoren van $\mathbb{R}^n$ zijn, dan is
$\dotprod{\vec{a}}{\vec{b}}\ = \ a_1\cdot {{b}_1}+a_2\cdot {{b}_2}+ \cdots +a_n \cdot{{b}_n}$ De verificatie dat het standaardinproduct aan de eisen van een inproduct voldoet is recht toe recht aan.

Als we naar $\mathbb{R}^n$ verwijzen als een inproductruimte, zonder een specifiek inproduct te geven, dan bedoelen we dat het inproduct het standaardinproduct is.

Een andere manier om het standaardinproduct te beschrijven is in termen van kolomvectoren $\vec{a}$ en $\vec{b}$

$\dotprod{\vec{a}}{\vec{b}}\ = \vec{a}^\top\, \vec{b}$

Laat $V$ de verzameling continue reële functies zijn gedefinieerd op een interval $\ivcc{a}{b}$ . Dan is $V$ met de gewone puntsgewijze optelling en scalaire vermenigvuldiging een vectorruimte. Neem $f,g\in V$ en definieer
$\dotprod{f}{g} = \int_a^b f(x)\cdot {g(x)}\,\dd x$ Dit is een inproduct op $V$ . De bilineariteit en de symmetrie zijn makkelijk na te gaan. De derde eigenschap bewijzen we als volgt. Neem een functie $f$ in $V$ en stel dat deze functie niet gelijk is aan de nulfunctie. Dan bestaat er een $\alpha$ in het interval $\ivcc{a}{b}$ zodanig dat $f(\alpha)\neq 0$ . Vanwege de continuiteit van $f$ is er een open interval om $\alpha$ heen zó dat $|f(x)|\gt \frac{1}{2}\cdot |f(\alpha)|\gt 0$ voor alle $x$ in dat interval. We laten $\delta$ de lengte zijn van dit interval. Dan geldt vanwege restrictie van de integraal tot het interval rond $\alpha$
$\dotprod{f}{f} = \int_a^b f(x)^2\dd x\geq \frac14\delta\cdot f(\alpha )^2\gt 0$ Dus als $\dotprod{f}{f} = \ 0$ dan is noodzakelijkerwijs $f(x) = 0$ voor alle $x\in\ivcc{a}{b}$ .

Door de symmetrie hoeven we slechts lineariteit in $\vec{a}$ te eisen; lineariteit in $\vec{b}$ , en dus bilineariteit, volgt dan automatisch.

De waarde $0$ wordt niet alleen aangenomen als $\vec{a}=\vec{b}=\vec{0}$ , maar ook als één van de twee argumenten gelijk is aan $\vec{0}$ :

$\dotprod{\vec{a}}{\vec{0}} = \dotprod{\vec{0}}{\vec{b}} = 0$ Dit volgt uit de bilineariteit van het inproduct. Bovendien zijn er ook situaties waar beide vectoren niet gelijk zijn aan $\vec{0}$ maar het inproduct wel $0$ is. Kijk maar bijvoorbeeld naar het inproduct van de vectoren $\rv{0,1}$ en $\rv{1,0}$ in de vectorruimte $\mathbb{R}^2$ met het standaardinproduct. Als twee vectoren inproduct $0$ hebben, noemen we deze vectoren orthogonaal of loodrecht. We zullen hier later uitgebreid op ingaan.

Omdat $\dotprod{\vec{a}}{\vec{a}}$ voor iedere vector $\vec{a}$ in een inproductruimte een niet-negatief reëel getal is, is $\sqrt{\dotprod{\vec{a}}{\vec{a}}}$ een goed gedefinieerde uitdrukking. Hiermee definiëren we lengte:

In een inproductruimte wordt de lengte of norm van een vector $\vec{a}$ gedefinieerd door
$\norm{\vec{a}}=\sqrt{\dotprod{\vec{a}}{\vec{a}}}$ De afstand tussen de vectoren $\vec{a}$ en $\vec{b}$ is per definitie de lengte van de verschilvector $\vec{a}-\vec{b}$ , dat wil zeggen: $\norm{\vec{a} -\vec{b}}$ .

Standaardinproduct

De lengte van $\rv{1,1,1,1}\in \mathbb{R}^4$ met het standaardinproduct is gelijk aan
$\sqrt{1^2+1^2+1^2+1^2}=\sqrt{4}=2$ De afstand tussen $\rv{2,1,3,4}$ en $\rv{5,1,7,4}$ is
$\sqrt{(2-5)^2 + (1-1)^2 + (3-7)^2 + (4-4)^2}=\sqrt{9+16}=5$

Inproduct van functies

In de inproductruimte $V$ met bovenstaand inproduct van functies op het interval $\ivcc{a}{b} = \ivcc{0}{1}$ is de lengte van de functie $f(x) = x^2$ gelijk aan
$\norm{f}=\sqrt{\int_0^1 x^2 \cdot x^2 \, \dd x}=\sqrt{\left[\frac15 x^5\right]_0^1}=\frac{1}{5}\, \sqrt{5}$

Afstandsfunctie

In het algemeen heet een functie $d(\vec{a},\vec{b})$ van de twee variabelen $\vec{a}$ en $\vec{b}$ uit dezelfde vectorruimte een afstandsfunctie als aan de volgende drie eigenschappen voldaan is voor alle vectoren $\vec{a}$ , $\vec{b}$ en $\vec{c}$ :

positiviteit: $d(\vec{a},\vec{b}) \ge 0$ met gelijkheid dan en slechts dan als $\vec{a}=\vec{b}$
symmetrie: $d(\vec{a},\vec{b}) =d(\vec{b},\vec{a})$
driehoeksongelijkheid: $d(\vec{a},\vec{c})\le d(\vec{a},\vec{b}) + d(\vec{b},\vec{c})$

De functie $d(\vec{a},\vec{b})=\norm{\vec{a}-\vec{b}}$ is een afstandsfunctie: de positiviteit volgt uit de positiviteit van het inproduct. De symmetrie volgt uit de bilineariteit van het inproduct: $\begin{array}{rcl}d(\vec{b},\vec{a})&=&\norm{\vec{b}-\vec{a}}\\ &=&\norm{-(\vec{a}-\vec{b})}\\&=&\sqrt{\dotprod{(-(\vec{a}-\vec{b}))}{(-(\vec{a}-\vec{b}))}}\\&=&\sqrt{(-1)^2\cdot \dotprod{(\vec{a}-\vec{b})}{(\vec{a}-\vec{b})}}\\ & =&\norm{\vec{a}-\vec{b}}\\ &=&d(\vec{a},\vec{b}) \end{array}$ De driehoeksongelijkheid wordt later bewezen.

Later zullen we bewijzen dat de norm de volgende interessante eigenschappen heeft. Hierbij is $\vec{v}$ een vector in een inproductruimte $V$ en is $\lambda$ een scalar.

$\norm{\lambda\vec{v}}= \abs{\lambda} \,\cdot \parallel \vec{v} \parallel$
$\norm{\vec{v}}\ge 0$
$\norm{\vec{v}}=0$ dan en slechts dan als $\vec{v}=0$

Onderstaande formule laat zien dat een inproduct uniek bepaald is door de lengte.

In een inproductruimte geldt de volgende formule voor alle vectoren $\vec{a}$ en $\vec{b}$ .

$\dotprod{\vec{a}}{\vec{b}} = \frac12\left(\norm{\vec{a} +\vec{b}}^2-\norm{\vec{a}}^2-\norm{\vec{b}}^2 \right)$

We werken het rechter lid uit om op het linker lid uit te komen:

$\begin{array}{rcl}\dfrac12\left(\norm{\vec{a} +\vec{b}}^2-\norm{\vec{a}}^2-\norm{\vec{b}}^2\right) &=&\dfrac12\left(\dotprod{(\vec{a} +\vec{b}) }{(\vec{a} +\vec{b})}-\dotprod{\vec{a} }{\vec{a} }-\dotprod{\vec{b} }{\vec{b} } \right) \\&&\phantom{xxx}\color{blue}{\text{definitie lengte}}\\&=&\dfrac12\left(\left(\dotprod{\vec{a}}{\vec{a}} +\dotprod{\vec{a}}{\vec{b} }+\dotprod{\vec{b} }{\vec{a}}+\dotprod{\vec{b}}{\vec{b}}\right)-\dotprod{\vec{a} }{\vec{a} }-\dotprod{\vec{b} }{\vec{b} } \right) \\&&\phantom{xxx}\color{blue}{\text{bilineariteit van het inproduct}}\\&=&\dfrac12\left(\dotprod{\vec{a}}{\vec{b}} +\dotprod{\vec{b} }{\vec{a}}\right) \\ &&\phantom{xxx}\color{blue}{\text{vereenvoudigd}}\\&=&\dfrac{1}{2}\left(\dotprod{\vec{a}}{\vec{b}}+\dotprod{\vec{a}}{\vec{b}}\right)\\ &&\phantom{xxx}\color{blue}{\text{symmetrie van het inproduct}}\\ &=&\dotprod{\vec{a} }{\vec{b} }\\ &&\phantom{xxx}\color{blue}{\text{vereenvoudigd}}\\ \end{array}$

Bekijk de vectorruimte $\mathbb{R}^3$ met het standaardinproduct.

Wat is het inproduct van de vectoren $\vec{x}=\rv{2,-2,2}$ en $\vec{y}=\rv{4,4,0}$ ?

$\dotprod{\vec{x}}{\vec{y}}=$ $0$

De waarde van het inproduct kan als volgt gevonden worden:
$\begin{array}{rcl} \dotprod{\vec{x}}{\vec{y}}&=&\dotprod{\rv{2,-2,2}}{\rv{4,4,0}}\\ &&\phantom{xx}\color{blue}{\text{vectoren uitgeschreven}}\\ &=&2\cdot 4-2\cdot4+2\cdot (0)\\ &&\phantom{xx}\color{blue}{\text{definitie standaardinproduct}}\\ &=&0\\ &&\phantom{xx}\color{blue}{\text{vereenvoudigd}} \end{array}$

Nieuw voorbeeld