Bullet loan

Sequences and series: Financial applications of sequences and series

Bullet loan

The theory on sequences and series provides a good starting point to discuss different types of loans. We will discuss loans that have terms of fixed length for the duration of the loan, where at the end of each term a fixed interest is paid over the remaining debt. The original debt is paid off with installments at the end of each period.

With a bullet loan, which we will discuss below, the installment is zero up to the last term. Two other types of loans, a linear loan and an annuity, are dealt with later. We will start with describing a general pattern.

Loans

When discussing loans we are always assuming a duration of #n# terms of fixed length (for example units like a month or a year), where at the beginning an amount #K# is borrowed, and the entire loan including interest must be paid off at the end of the duration #n#.

The interest is written as #p\%#. In many cases, we use the growth rate #i = \frac{p}{100}# instead of the percentage #p\%#. With all the loans we discuss, the interest over the remaining outstanding debt is paid at the end of a term.

We use the following notation, where #j# indicates a term (hence,#j=1,2,\ldots,n#):

#a_j# is the installment at the end of the #j#-th term
#r_j# is the interest payment at the end of the #j#-th term
#R_j# is the remaining outstanding debt at the end of the #j#-th term

The properties are:

#R_0=K#
#R_j = R_{j-1}-a_j#
#R_n = 0#
#\sum_{j=1}^na_j =K#
#r_j = R_{j-1}\cdot i#

The formula #R_0=K# expresses the fact that at the end of the #0#-th term, or at the beginning of the loan, the remaining outstanding debt is equal to #K#, the initial borrowed amount.
At the end of term #j# the remaining outstanding debt is equal to the difference of the loan at the end of the previous term and the installment over that term, hence, #R_{j}=R_{j-1}-a_j#.
The formula #R_n=0# expresses the fact that at the end of the loan, the debt is paid off.
The sum #\sum_{j=1}^na_j# of all installments is equal to the amount that is borrowed: #K#.
At the end of term #j# one needs to pay #p\%# interest over the outstanding debt at the beginning of that term, hence, over the debt, #R_{j-1}#, at the end of the previous term. Therefore #r_j = \frac{p}{100}\cdot R_{j-1}=i\cdot R_{j-1}#.

If there would not have been an interest payment or payment to pay of the debt at the end of the duration, then the remaining outstanding debt will follow the exponential growth model: #R_j = K\cdot (1+i)^j# for #j\lt n#. This situation is only fitting in the model above if there's only one term #(n=1)#, since we assume that there's an interest payment at the end of each term. In that case #i# is the interest over the entire period and #K-a_1 =R_0-a_1 = R_1=0#, hence, #a_1=K# and #r_1=K\cdot i#.

The formula #\sum_{j=1}^na_j =K# is a result from the formulas above:

\[\begin{array}{rcl} \displaystyle\sum_{j=1}^na_j &=&(R_0-R_1)+(R_1-R_2)+\cdots (R_{n-1}-R_n)\\ &=&R_0-(R_1-R_1)-(R_2-R_2))-\cdots- (R_{n-1}-R_{n-1})-R_n\\ &=&R_0-R_n\\ &=&K-0\\ &=&K\end{array}\]

The formulas indicate that, for a loan with given growth rate #i#, initial amount #K# and duration #n#, all remaining debts #R_j# and all interest payments #r_j# are known once the installments #a_j# are known. The different types of loans depend on this. We will take a closer look at three types of loans:

Bullet loan: no installments in the terms in between
Linear loan: constant installment per term
Annuity: constant sum of installment and interest per term

We will discuss each of these loans separately. Here we take a look at the first, most simple one.

Bullet loan

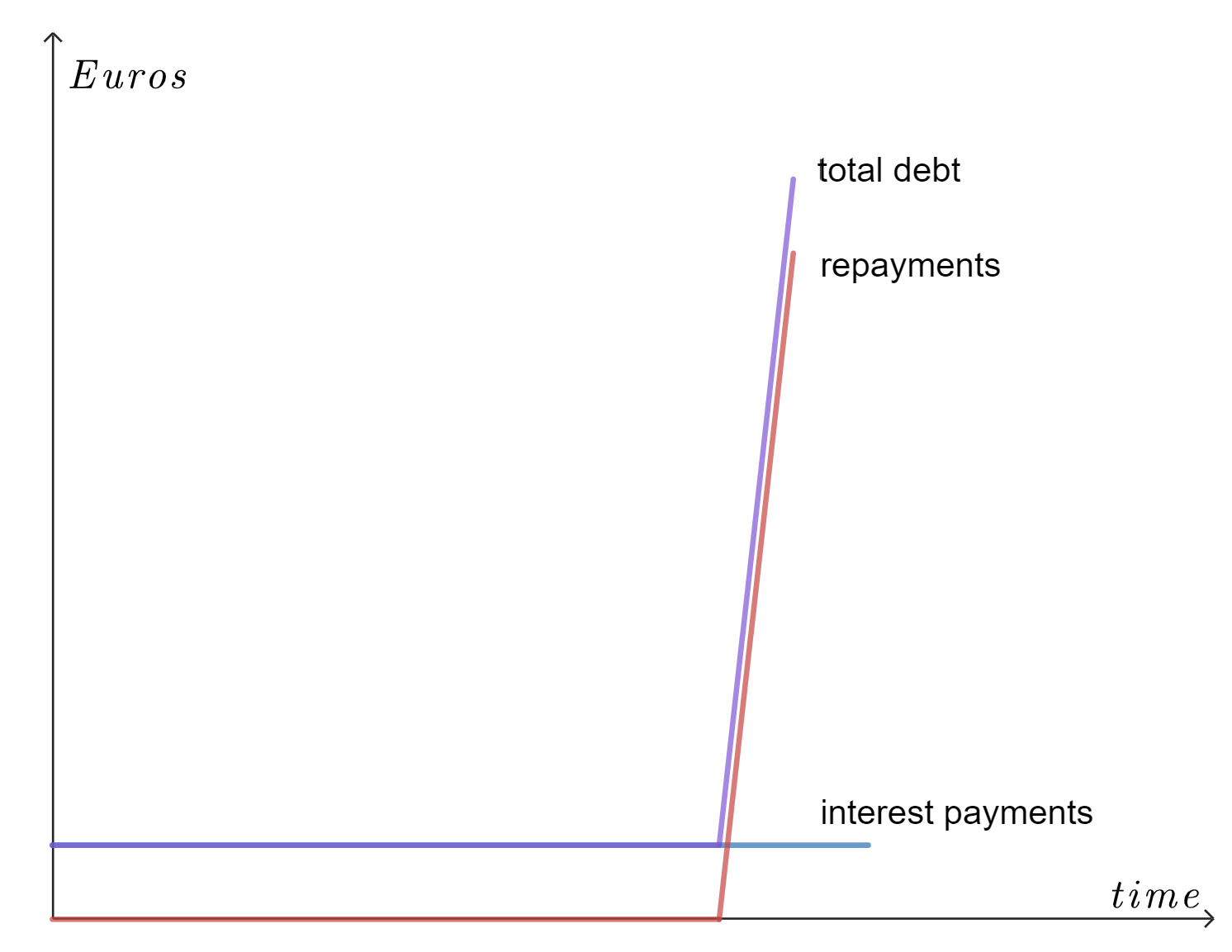
A bullet loan is a loan with no intermediate installments. The interest of #p\%# (or growth rate #i=\frac{p}{100}#) is paid at the end of each term. The initial loan (#K#) is paid back entirely at the end of the duration (#n#).

Hence, a bullet loan is characterized by the following formulas:

\[\begin{array}{rcl}\text{Installments}&&a_1 = a_2 = a_3 =\cdots = a_{n-1} = 0\\ &&a_n = K\\ \text{Interest payments }&& r_1 = r_2 = r_3 =\cdots = r_n = K\cdot i\\ \text{Remaining debt }&&R_1 = R_2 = R_3 =\cdots = R_{n-1} = K\\ &&R_n = 0\end{array}\]

Since there are no intermediate installments, one needs to pay interest on the entire initial loan, during the whole duration.

This type of loan is characterized by relative low payments during the duration and a very high payment at the end of the duration.

A 10%-bullet loan of €100,000 with a duration of 10 years, leads to the following table.

Term	Debt at start	Interest payment	Installment	Debt at end
#j#	#R_{j-1}#	#r_j#	#a_j#	#R_j#
1	100,000	10,000	0	100,000
2	100,000	10,000	0	100,000
3	100,000	10,000	0	100,000
4	100,000	10,000	0	100,000
5	100,000	10,000	0	100,000
6	100,000	10,000	0	100,000
7	100,000	10,000	0	100,000
8	100,000	10,000	0	100,000
9	100,000	10,000	0	100,000
10	100,000	10,000	100,000	0

In a graph:

For each type of loan we discuss, the interest payment satisfies #r_j = R_{j-1}\cdot i#. In this case we have#R_{j-1}=K# for each #j#, dus #r_j=K\cdot i#.

Examples

Given a 10%-bullet loan of #\euro\,##50000# with a duration of #12# years.

Calculate the interest payment in term #7#.

#r_{7} =# #5000#

Given:

initial borrowed capital: #C = 50000#
interest: #i = 0.10#
duration: #n = 12#
term: #j = 7#

Since there are no intermediate installments, one needs to pay interest on the entire initial borrowed capital each term. This can be calculated as follows:
\[\begin{array}{rcl}
r_j &=& C\cdot i\\\
&&\phantom{xxxxx}\color{blue}{\text{formula for interest payment of a bullet loan in term }j}\\
r_{7} &=& 50000\cdot 0.10\\
&&\phantom{xxxxx}\color{blue}{\text{value for }j,\ K\text{ and }i\text{ entered}}\\
&=& 5000\\
&&\phantom{xxxxx}\color{blue}{\text{calculated}}\\
\end{array}\]

New example