Linear loan

Sequences and series: Financial applications of sequences and series

Linear loan

Here we discuss the linear loan. We will use the same notation as with the bullet loan. In particular, #C# is the borrowed capital, #a_j# indicates the installment in term #j# and #r_j# the interest payment in that term. The duration is #n# terms. The size of the interest payment is determined by the interest rate #i#.

Linear loan

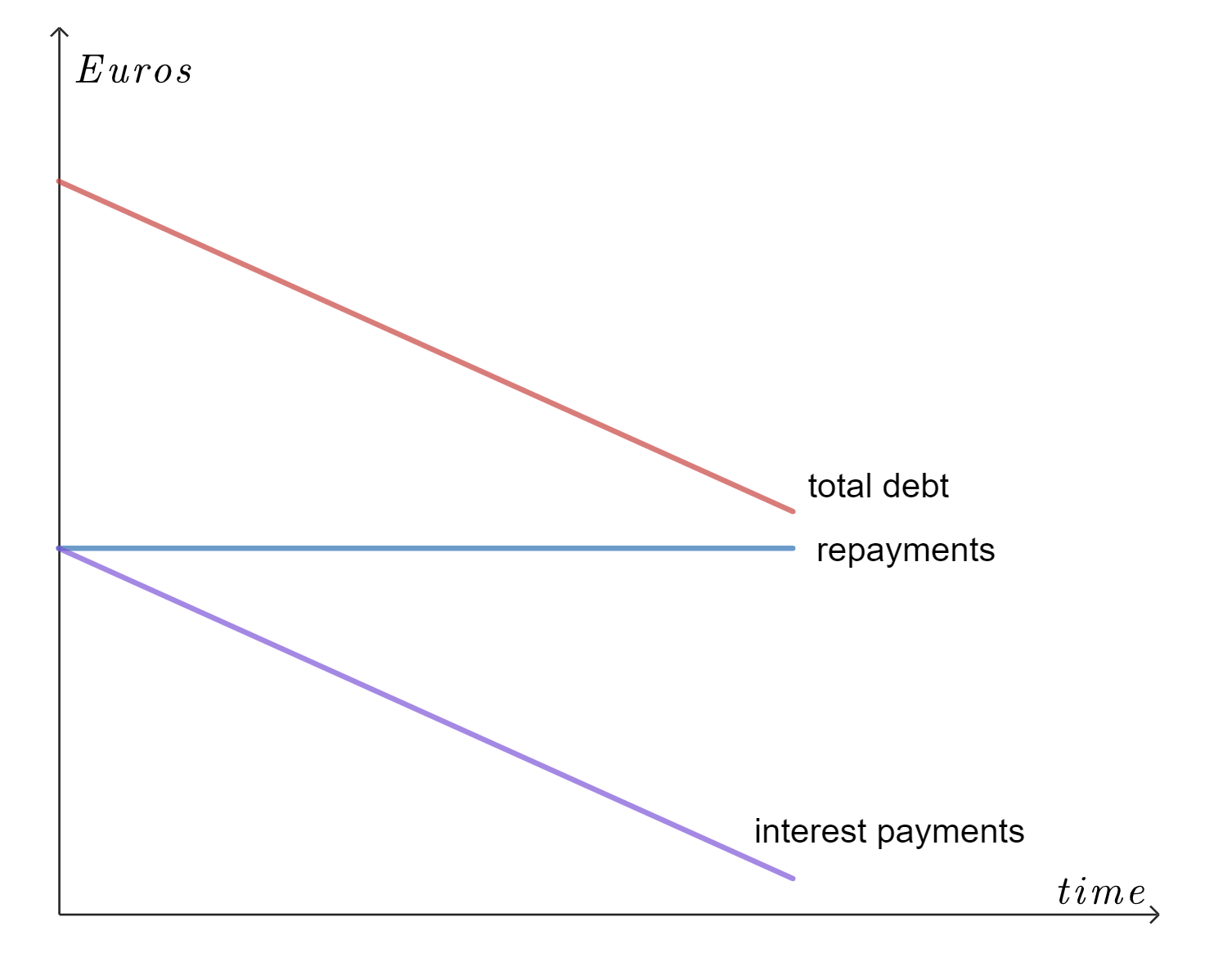
With a linear loan the installments are distributed evenly along the total duration. At the end of each term a fixed part of the total loan is paid back.

Hence, the loan is characterized by the following formulas.

\[\begin{array}{rcl}\text{Installments}&&a_{j} =\dfrac{C}{n}\\ \text{Interest payments}&& r_j=\dfrac{n-j+1}{n} \cdot C \cdot i\\ \text{Remaining debt}&&R_j =\dfrac{n-j}{n} \cdot C\\ \end{array}\]

Since the remaining debt becomes smaller each term, one needs to pay less interest than the previous term. The payments are relatively high at the beginning of the duration, but become lower as time passes.

#r_1 \gt r_2 \gt r_3 \cdots \gt r_n#

A 10%-linear loan of €100,000 with a duration of 10 years leads to the following payments table.

Term	Debt at start	Interest payment	Installment	Debt at end
#j#	#R_{j-1}#	#r_j#	#a_j#	#R_j#
1	100,000	10,000	10,000	90,000
2	90,000	9,000	10,000	80,000
3	80,000	8,000	10,000	70,000
4	70,000	7,000	10,000	60,000
5	60,000	6,000	10,000	50,000
6	50,000	5,000	10,000	40,000
7	40,000	4,000	10,000	30,000
8	30,000	3,000	10,000	20,000
9	20,000	2,000	10,000	10,000
10	10,000	1,000	10,000	0

In a graph:

In term #j# the same amount is paid back as in all other terms. Since there are #n# terms and at the end we need to have the total debt of #C# paid off, we have #n\cdot a_j = C#, such that #a_j = \dfrac{C}{n}#.

At the end of that term #j# but before the payment in that term, there have been #j-1# installments. The remaining outstanding debt then is \[R_{j-1} = C-(j-1)\cdot a_j = C - (j-1)\cdot \dfrac{C}{n} = \frac{n-j+1}{n}\cdot C\] At the end of term #j# an interest payment of \[r_j = R_{j-1}\cdot i = \frac{n-j+1}{n}\cdot C\cdot i\] is made. After paying, the remaining outstanding debt is \[R_j = C-j\cdot a_j = \frac{n-j}{n}\cdot C\]

With this we have derived the formulas for the linear loan.

Given a 4%-linear loan of #\euro\,##140000# with a duration of #18# years.

Calculate the interest payment in year #3#, rounded to two decimals.

#r_{3} =# #4977.78#

Given:

initial borrowed capital: #C = 140000#
interest: #i = 0.04#
duration: #n = 18#
term: #j = 3#

To calculate the interest payment in term #3# we use the following formula:
\[\begin{array}{rcl}
r_j &=& \dfrac{n-(j-1)}{n}\cdot C\cdot i\\
&&\phantom{xxxxx}\color{blue}{\text{formula interest payment linear loan }}\\
r_{3} &=& \dfrac{18-(3-1)}{18}\cdot 140000\cdot 0.04\\
&&\phantom{xxxxx}\color{blue}{\text{values for }n, j, C\text{ and }i\text{ entered }}\\
&=& 4977.78\\
&&\phantom{xxxxx}\color{blue}{\text{calculated}}\\
\end{array}\]

New example