Negative exponents

Basic algebra skills: Negative exponents

Negative exponents

So far we have seen both linear functions and equations, and quadratic functions and equations. Now, we will look at functions and equations with negative exponents. We start with a calculation rule.

Calculation rule for negative exponents

For unknown #x# and a number #n#, we have

\[x^{-n}=\frac{1}{x^n}\]

This means that #x^{-1}=\frac{1}{x}# and #x^{-2}=\frac{1}{x^2}#.

This rule applies not only to functions but also to numbers. For example:

\[\frac{1}{2}=2^{-1}\]

Quotient functions

The product #(x+2)\cdot(x+3)^{-1}# is equal to the quotient function #\frac{x+2}{x+3}#.

Unlike linear and quadratic functions, functions with a negative exponent are not defined everywhere. This means that not all #x# values have a corresponding #f(x)# value. To illustrate, we will look at the function #\frac{1}{x}#. The graph of the #y=\frac{1}{x}# function is shown below.

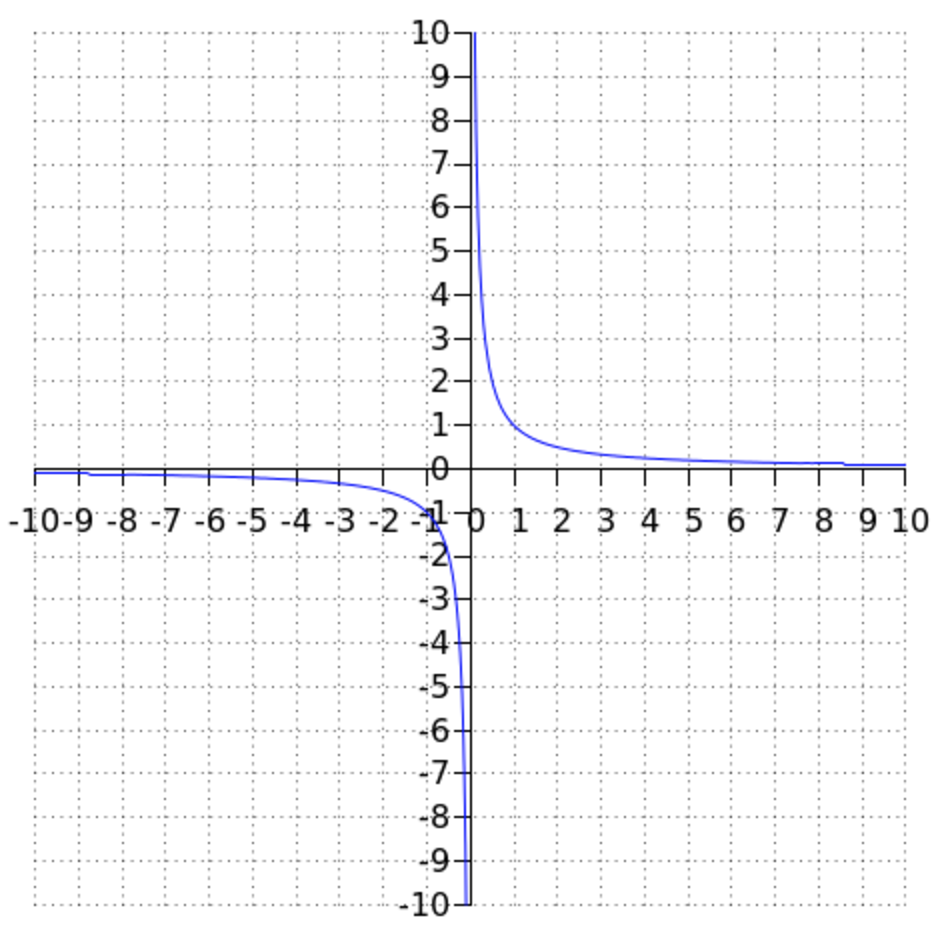
The function #\frac{1}{x}# is defined for all real numbers #x\ne0#. In #x=0#, the denominator is equal to #0#, and the fraction in the function statement is therefore not defined. Near #x=0#, the function values are very far from #0#:

Hyperbola and asymptote

To the right of #x=0#, the function #\frac{1}{x}# goes to infinity (#\infty#); that is, you can get arbitrarily large numbers as function values by choosing #x# to be positive and close enough to #0#. Likewise, the function to the left of #x=0# goes to negative infinity (#-\infty#). We can conclude that the graph of #\frac{1}{x}# comes arbitrarily close to the #y#-axis. In other words: the #y#-axis is a vertical asymptote of the graph (we also say: of the function).

The #x#-axis is a horizontal asymptote of the graph: as we let #x# approach infinity, #\dfrac{1}{x}# gets smaller and smaller and the function value gets closer to #0#. We find points of the graph that are arbitrarily close to the #x#-axis, but not on it. The same applies if we let #x# go to negative infinity; even then, #\dfrac{1}{x}# comes closer and closer to #0# without being equal to it.

The graph of #\frac{1}{x}# is sometimes called a hyperbola. A characteristic of the hyperbola is the pair of lines that the graph gets closer and closer to without intersecting them. These lines are called asymptotes.

Orthogonal

In general, the asymptotes of a hyperbola do not have to be perpendicular to each other, as is the case with the #\frac{1}{x}# graph. If they are perpendicular, then we call the hyperbola orthogonal.

Example

We say that the constant function #y=4# has no asymptote: the values of the function are arbitrarily close to #4#; they are the same. Because in the definition of asymptote we exclude the possibility that the value becomes equal (or, more generally, that the points of the graph lie on the asymptote), we do not speak of an asymptote.

Which of the following statements is/are true for all real numbers #x# unequal to #0#?

The following statements are true:

#\frac{3}{x}=3\cdot x^{-1}#
#\frac{1}{4 \cdot x^2}=\frac{1}{4} \cdot x^{-2}#

The following statements are not true:

#\frac{1}{9 \cdot x}\ne 9 \cdot x^{-1}#, because #\frac{1}{9 \cdot x}=\frac{1}{9} \cdot x^{-1}#
#\frac{3}{x^2} \ne \frac{1}{3}\cdot x^{-2}#, because #\frac{3}{x^2}=3\cdot x^{-2}#

New example